How to find whether lines are parallel
Help Questions
SSAT Upper Level: Quantitative › How to find whether lines are parallel

Figure NOT drawn to scale
In the above figure, 


Explanation
The two marked angles are same-side interior angles of two parallel lines formed by a transversal 
Solve for 

Figure NOT drawn to scale
In the above figure, 

Explanation
Angles of degree measures 

Solving for 
The angles of measures 

Substituting for 

Figure NOT drawn to scale
In the above figure, 

Explanation
The two marked angles are same-side exterior angles of two parallel lines formed by a transversal 
Line A has equation 
Line B has equation 
Which statement is true of the two lines?
Explanation
Write each statement in slope-intercept form:
Line A:
The slope is 
Line B:
The slope is 
The lines have differing slopes, so they are neither identical nor parallel. The product of the slopes is 
Line P passes through the origin and point 
Line Q passes through the origin and point 
Line R passes through the origin and point 
Line S passes through the origin and point 
Which of these lines is parallel to the line of the equation 
Line S
Line R
Line P
Line Q
None of the other responses is correct.
Explanation
First, find the slope of the line of the equation 
The slope of this line is 
Find the slopes of all four lines by using the slope formula 
using the other point.
Line P:
Line Q:
Line R:
Line S:
Line S has the desired slope and is the correct choice.
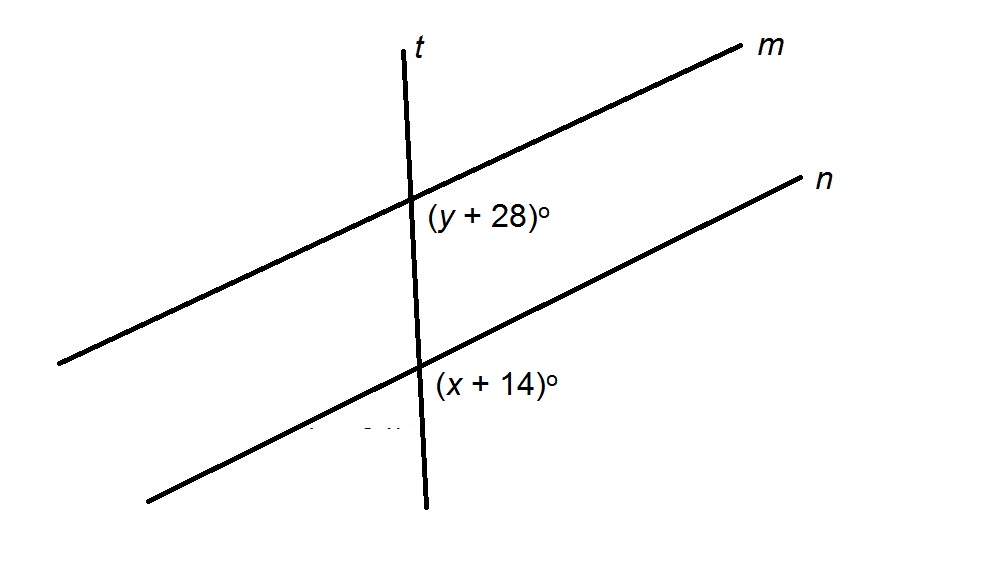
Figure NOT drawn to scale
In the above figure, 


Explanation
The two marked angles are corresponding angles of two parallel lines formed by a transversal, so the angles are congruent. Therefore,
Solving for 
You are given three lines as follows:
Line A includes points 

Line B includes point 


Line C includes the origin and point 
Which lines are parallel?
Explanation
Find the slope of all three lines using the slope formula 
Line A:
Line B:
Line C:
Lines A and C have the same slope; Line B has a different slope. Only Lines A and C are parallel.































































