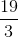SSAT Upper Level Quantitative - How to find slope

What is the slope of the line that passes through the points $(-1,4) \text{ and } (-5,1)$ ?

$\frac{3}{4}$

$-\frac{3}{4}$

$\frac{4}{3}$

$-\frac{4}{3}$

Explanation

Use the following formula to find the slope:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Substituting the values from the points given, we get the following slope:

$\text{Slope}=\frac{1-4}{-5-(-1)}=\frac{-3}{-4}=\frac{3}{4}$

Find the slope of a line that passes through the points and .

$\frac{3}{19}$

$\frac{19}{3}$

$-\frac{3}{19}$

$-\frac{19}{3}$

Explanation

To find the slope of the line that passes through the given points, you can use the slope equation.

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

$\text{Slope}=\frac{-1-2}{-2-17}=\frac{-3}{-19}=\frac{3}{19}$

What is the slope of the line with the equation

$-\frac{2}{3}$

$-\frac{3}{2}$

Explanation

To find the slope, put the equation in the form of .

$y=-\frac{2}{3}x-3$

Since $m=-\frac{2}{3}$ , that is the value of the slope.

Find the slope of the line that passes through the points and .

$\frac{3-b}{2-a}$

$\frac{2-a}{3-b}$

$\frac{2-b}{3-a}$

$\frac{3-a}{2-b}$

Explanation

To find the slope of the line that passes through the given points, you can use the slope equation.

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

$\text{Slope}=\frac{3-b}{2-a}$

Find the slope of the following function:

$\frac{1}{3}$

Explanation

Rewrite the equation in slope-intercept form, .

$\frac{2x-3}{6}=y$

$y=\frac{1}{3}x-\frac{1}{2}$

The slope is the term, which is $\frac{1}{3}$ .

Find the slope of the line that goes through the points and .

$\frac{17s}{2t}$

$\frac{-s}{6t}$

$\frac{2t}{17s}$

$\frac{6t}{-s}$

Explanation

Even though there are variables involved in the coordinates of these points, you can still use the slope formula to figure out the slope of the line that connects them.

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

$\text{Slope}=\frac{-9s-8s}{2t-4t}=\frac{-17s}{-2t}=\frac{17s}{2t}$

Consider the line of the equation . The line of a function has the same slope as that of . Which of the following could be the definition of ?

Explanation

The definition of is written in slope-intercept form , in which , the coefficient of , is the slope of its line. , so the slope of its line is .

We must select the choice whose line has this slope. The definition of in each choice is also written in slope-intercept form, so we select the alternative with -coefficient 5; the only such alternative is .

Find the slope of the line that passes through the points and .

$-\frac{1}{4}$

$\frac{1}{4}$

Explanation

You can use the slope formula to figure out the slope of the line that connects these two points. Just substitute the specified coordinates into the equation and then subtract:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$