Cubes
Help Questions
PSAT Math › Cubes
A rectangular prism has a volume of 144 and a surface area of 192. If the shortest edge is 3, what is the length of the longest diagonal through the prism?
Explanation
The volume of a rectangular prism is 
We are told that the shortest edge is 3. Let us call this the height.
We now have 

Now we replace variables by known values:
Now we have:
We have thus determined that the other two edges of the rectangular prism will be 4 and 12. We now need to find the longest diagonal. This is equal to:
If you do not remember how to find this directly, you can also do it in steps. You first find the diagonal across one of the sides (in the plane), by using the Pythagorean Theorem. For example, we choose the side with edges 3 and 4. This diagonal will be:
We then use a plane with one side given by the diagonal we just found (length 5) and the other given by the distance of the 3rd edge (length 12).
This diagonal is then 
A certain cube has a side length of 25 m. How many square tiles, each with an area of 5 m2, are needed to fully cover the surface of the cube?
100
200
500
750
1000
Explanation
A cube with a side length of 25m has a surface area of:
25m * 25m * 6 = 3,750 m2
(The surface area of a cube is equal to the area of one face of the cube multiplied by 6 sides. In other words, if the side of a cube is s, then the surface area of the cube is 6_s_2.)
Each square tile has an area of 5 m2.
Therefore, the total number of square tiles needed to fully cover the surface of the cube is:
3,750m2/5m2 = 750
Note: the volume of a cube with side length s is equal to _s_3. Therefore, if asked how many mini-cubes with side length n are needed to fill the original cube, the answer would be:
s3/n3
A rectangular prism has a volume of 144 and a surface area of 192. If the shortest edge is 3, what is the length of the longest diagonal through the prism?
Explanation
The volume of a rectangular prism is 
We are told that the shortest edge is 3. Let us call this the height.
We now have 

Now we replace variables by known values:
Now we have:
We have thus determined that the other two edges of the rectangular prism will be 4 and 12. We now need to find the longest diagonal. This is equal to:
If you do not remember how to find this directly, you can also do it in steps. You first find the diagonal across one of the sides (in the plane), by using the Pythagorean Theorem. For example, we choose the side with edges 3 and 4. This diagonal will be:
We then use a plane with one side given by the diagonal we just found (length 5) and the other given by the distance of the 3rd edge (length 12).
This diagonal is then 
A certain cube has a side length of 25 m. How many square tiles, each with an area of 5 m2, are needed to fully cover the surface of the cube?
100
200
500
750
1000
Explanation
A cube with a side length of 25m has a surface area of:
25m * 25m * 6 = 3,750 m2
(The surface area of a cube is equal to the area of one face of the cube multiplied by 6 sides. In other words, if the side of a cube is s, then the surface area of the cube is 6_s_2.)
Each square tile has an area of 5 m2.
Therefore, the total number of square tiles needed to fully cover the surface of the cube is:
3,750m2/5m2 = 750
Note: the volume of a cube with side length s is equal to _s_3. Therefore, if asked how many mini-cubes with side length n are needed to fill the original cube, the answer would be:
s3/n3
If a cube has an area of 
Explanation
The area of a cube is equal to the measure of one edge cubed. If we take the cube root of 




There are 
If a cube has an area of 
Explanation
The area of a cube is equal to the measure of one edge cubed. If we take the cube root of 




There are 
If a cube has a surface area of 
Explanation
If the surface area is 



If a cube has a surface area of 
Explanation
If the surface area is 



If the volume of a cube is 64 cubic inches, then it has an edge length of .
4 in
8 in
9 in
6 in
2 in
Explanation
If the volume of a cube is 64 cubic inches, then it has an edge length of .
4 in
8 in
9 in
6 in
2 in
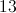

























![side=\sqrt[3]{64}=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/227989/gif.latex)