Quadrilaterals
Help Questions
PSAT Math › Quadrilaterals

Refer to the above diagram. 
Give the area of Quadrilateral 
Explanation



By the Angle-Angle Similarity Postulate, since
and


and since corresponding sides of similar triangles are in proportion,

The smaller base is 

The area of the trapezoid is

Refer to the above diagram. 
Give the area of Quadrilateral 
Explanation



By the Angle-Angle Similarity Postulate, since
and


and since corresponding sides of similar triangles are in proportion,

The smaller base is 

The area of the trapezoid is
In Rhombus 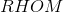








Explanation
The figure referenced is below.

Consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so
A diagonal of a rhombus bisects its angles, so
A similar argument proves that 
Since all three angles of 

In Rhombus 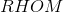








Explanation
The figure referenced is below.

Consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so
A diagonal of a rhombus bisects its angles, so
A similar argument proves that 
Since all three angles of 

In Rhombus 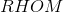








Explanation
The figure referenced is below.

Consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so
A diagonal of a rhombus bisects its angles, so
A similar argument proves that 
Since all three angles of 


Refer to the above diagram. 
Give the area of Quadrilateral 
Explanation



By the Angle-Angle Similarity Postulate, since
and


and since corresponding sides of similar triangles are in proportion,

The smaller base is 

The area of the trapezoid is
If the area of a rhombus is 24 and one diagonal length is 6, find the perimeter of the rhombus.
24
20
16
12
8
Explanation
The area of a rhombus is found by
A = 1/2(_d_1)(_d_2)
where _d_1 and _d_2 are the lengths of the diagonals. Substituting for the given values yields
24 = 1/2(_d_1)(6)
24 = 3(_d_1)
8 = _d_1
Now, use the facts that diagonals are perpendicular in a rhombus, diagonals bisect each other in a rhombus, and the Pythagorean Theorem to determine that the two diagonals form 4 right triangles with leg lengths of 3 and 4. Since 32 + 42 = 52, each side length is 5, so the perimeter is 5(4) = 20.
If the area of a rhombus is 24 and one diagonal length is 6, find the perimeter of the rhombus.
24
20
16
12
8
Explanation
The area of a rhombus is found by
A = 1/2(_d_1)(_d_2)
where _d_1 and _d_2 are the lengths of the diagonals. Substituting for the given values yields
24 = 1/2(_d_1)(6)
24 = 3(_d_1)
8 = _d_1
Now, use the facts that diagonals are perpendicular in a rhombus, diagonals bisect each other in a rhombus, and the Pythagorean Theorem to determine that the two diagonals form 4 right triangles with leg lengths of 3 and 4. Since 32 + 42 = 52, each side length is 5, so the perimeter is 5(4) = 20.
If the area of a rhombus is 24 and one diagonal length is 6, find the perimeter of the rhombus.
24
20
16
12
8
Explanation
The area of a rhombus is found by
A = 1/2(_d_1)(_d_2)
where _d_1 and _d_2 are the lengths of the diagonals. Substituting for the given values yields
24 = 1/2(_d_1)(6)
24 = 3(_d_1)
8 = _d_1
Now, use the facts that diagonals are perpendicular in a rhombus, diagonals bisect each other in a rhombus, and the Pythagorean Theorem to determine that the two diagonals form 4 right triangles with leg lengths of 3 and 4. Since 32 + 42 = 52, each side length is 5, so the perimeter is 5(4) = 20.
The two rectangles shown below are similar. What is the length of EF?

5
6
8
10
Explanation
When two polygons are similar, the lengths of their corresponding sides are proportional to each other. In this diagram, AC and EG are corresponding sides and AB and EF are corresponding sides.
To solve this question, you can therefore write a proportion:
AC/EG = AB/EF ≥ 3/6 = 5/EF
From this proportion, we know that side EF is equal to 10.