PSAT Math - How to find the slope of perpendicular lines

Axes_1

Give the slope of a line perpendicular to the line in the above figure.

$-\frac{1}{2}$

$\frac{1}{2}$

None of the other responses is correct.

Explanation

In order to move from the upper left point to the lower right point, it is necessary to move down 3 units and right six units. This is a rise of and a run of 6. The slope of a line is the ratio of rise to run, so slope of the line shown is $\frac{-3}{6} = -\frac{1}{2}$ .

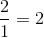
A line perpendicular to this will have a slope equal to the opposite of the reciprocal of $-\frac{1}{2}$ . This is $\frac{2} {1} = 2$ .

The equation of a line is: 8x + 16y = 48

What is the slope of a line that runs perpendicular to that line?

-2

-1/8

-1/4

Explanation

First, solve for the equation of the line in the form of y = mx + b so that you can determine the slope, m of the line:

8x + 16y = 48

16y = -8x + 48

y = -(8/16)x + 48/16

y = -(1/2)x + 3

Therefore the slope (or m) = -1/2

The slope of a perpendicular line is the negative inverse of the slope.

m = - (-2/1) = 2

A line passes through the points $(3,5)$ and $(4,7)$ . What is the equation for the line?

$y=2x-1$

$y=\frac{1}{2}x-1$

$y=\frac{1}{2}x+3.5$

$y=2x$

None of the available answers

Explanation

First we will calculate the slope as follows:

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{7-5}{4-3}=\frac{2}{1}=2$

And our equation for a line is

$y=mx+b=2x+b$

Now we need to calculate b. We can pick either of the points given and solve for $\dpi{100} b$

$5=2(3)+b$

$b=-1$

Our equation for the line becomes

$y=2x-1$

Screen_shot_2013-09-04_at_10.56.34_am

What is the equation of a line perpendicular to the one above, passing through the point ?

$y=-\frac{1}{3}x+\frac{8}{3}$

$y=-\frac{4}{3}x+2$

$y=\frac{4}{3}x-2$

$y=\frac{1}{3}x+\frac{4}{3}$

$y=-\frac{1}{2}x+3$

Explanation

Looking at the graph, we can tell the slope of the line is 3 with a $\dpi{100} y$ -intercept of , so the equation of the line is:

$y=3x-4$

A perpendicular line to this would have a slope of $-\frac{1}{3}$ , and would pass through the point so it follows:

$y=-\frac{1}{3}x+c\rightarrow 2=-\frac{1}{3}(2)+c\rightarrow c=8/3\rightarrow y=-\frac{1}{3}x+\frac{8}{3}$

Solve the equation for x and y.

5_x_² + y = 20

x_² + 2_y = 10

x = √10/3, –√10/3

y = 10/3

x = 14, 5

y = 4, 6

x = √4/5, 7

y = √3/10, 4

No solution

Explanation

The problem involves the same method used for the rest of the practice set. However since the x is squared we will have multiple solutions. Solve this one in the same way as number 2. However be careful to notice that the y value is the same for both x values. The graph below illustrates the solution.

Sat_math_165_06

Solve the equation for x and y.

x² + y = 31

x + y = 11

x = 5, –4

y = 6, 15

x = 6, 15

y = 5, –4

x = 8, –6

y = 13, 7

x = 13, 7

y = 8, –6

Explanation

Solving the equation follows the same system as the first problem. However since x is squared in this problem we will have two possible solutions for each unknown. Again substitute y=11-x and solve from there. Hence, x2+11-x=31. So x2-x=20. 5 squared is 25, minus 5 is 20. Now we know 5 is one of our solutions. Then we must solve for the second solution which is -4. -4 squared is 16 and 16 –(-4) is 20. The last step is to solve for y for the two possible solutions of x. We get 15 and 6. The graph below illustrates to solutions.

Sat_math_165_02

Line M passes through the points (2,2) and (3,–5). Which of the following is perpendicular to line M?

y = 7_x_ – 6

y = –7_x_ – 5

y = (1/7)x + 3

y = –(1/7)x – 1

y = 7_x_ + 4

Explanation

First we find the slope of line M by using the slope formula (_y_2 – _y_1)/(_x_2 – _x_1).

(–5 – 2)/(3 – 2) = –7/1. This means the slope of Line M is –7. A line perpendicular to Line M will have a negative reciprocal slope. Thus, the answer is y = (1/7)x + 3.

Solve the equation for x and y.

_x_² + y = 60

x – y = 50

x = 10, –11

y = –40, –61

x = 11, –10

y = 40, 61

x = –40, –61

y = 10, –11

x = 40, 61

y = 11, –10

Explanation

This is a system of equations problem with an x squared, to be solved just like the rest of the problem set. Two solutions are required due to the x2. The graph below illustrates those solutions.

Sat_math_165_10

Two points on line m are (3,7) and (-2, 5). Line k is perpendicular to line m. What is the slope of line k?

2/5

-5

-5/2

Explanation

The slope of line m is the (y2 - y1) / (x2 - x1) = (5-7) / (-2 - 3)

= -2 / -5

= 2/5

To find the slope of a line perpendicular to a given line, we must take the negative reciprocal of the slope of the given line.

Thus the slope of line k is the negative reciprocal of 2/5 (slope of line m), which is -5/2.

Solve the equation for x and y.

x² – y = 96

x + y = 14

x = 25, 4

y = 10, –11

x = 15, 8

y = 5, –14

x = 10, –11

y = 25, 4

x = 5, –14

y = 15, 8

Explanation

This problem is very similar to number 2. Derive y=14-x and solve from there. The graph below illustrates the solution.

Sat_math_165_03

How to find the slope of perpendicular lines

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation