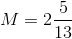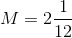Geometry
Help Questions
PSAT Math › Geometry

Note: Figure NOT drawn to scale.
The above polygon has perimeter 190. Evaluate 
Explanation
To get the expression equivalent to the perimeter, add the lengths of the sides:
Since the perimeter is 190, we can simplify this to
and solve as follows:

Note: Figure NOT drawn to scale.
The above polygon has perimeter 190. Evaluate 
Explanation
To get the expression equivalent to the perimeter, add the lengths of the sides:
Since the perimeter is 190, we can simplify this to
and solve as follows:

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 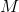
Explanation
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for 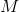

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 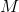
Explanation
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for 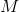
A regular tetrahedron has an edge length of 
Explanation
The volume of a tetrahedron is found with the equation 

Plug in 4 for the edge length and reduce as much as possible to find the answer:
The volume of the tetrahedron is 
One line has four collinear points in order from left to right A, B, C, D. If AB = 10’, CD was twice as long as AB, and AC = 25’, how long is AD?
45'
40'
50'
35'
30'
Explanation
AB = 10 ’
BC = AC – AB = 25’ – 10’ = 15’
CD = 2 * AB = 2 * 10’ = 20 ’
AD = AB + BC + CD = 10’ + 15’ + 20’ = 45’
A circle with a radius of five is centered at the origin. A point on the circumference of the circle has an x-coordinate of two and a positive y-coordinate. What is the value of the y-coordinate?
Explanation
Recall that the general form of the equation of a circle centered at the origin is:
_x_2 + _y_2 = _r_2
We know that the radius of our circle is five. Therefore, we know that the equation for our circle is:
_x_2 + _y_2 = 52
_x_2 + _y_2 = 25
Now, the question asks for the positive y-coordinate when x = 2. To solve this, simply plug in for x:
22 + _y_2 = 25
4 + _y_2 = 25
_y_2 = 21
y = ±√(21)
Since our answer will be positive, it must be √(21).

Note: Figure NOT drawn to scale.
The above polygon has perimeter 190. Evaluate 
Explanation
To get the expression equivalent to the perimeter, add the lengths of the sides:
Since the perimeter is 190, we can simplify this to
and solve as follows:
A rectangular prism has a volume of 144 and a surface area of 192. If the shortest edge is 3, what is the length of the longest diagonal through the prism?
Explanation
The volume of a rectangular prism is 
We are told that the shortest edge is 3. Let us call this the height.
We now have 

Now we replace variables by known values:
Now we have:
We have thus determined that the other two edges of the rectangular prism will be 4 and 12. We now need to find the longest diagonal. This is equal to:
If you do not remember how to find this directly, you can also do it in steps. You first find the diagonal across one of the sides (in the plane), by using the Pythagorean Theorem. For example, we choose the side with edges 3 and 4. This diagonal will be:
We then use a plane with one side given by the diagonal we just found (length 5) and the other given by the distance of the 3rd edge (length 12).
This diagonal is then 

What is the equation of the line in the graph above?
Explanation
In order to find the equation of a line in slope-intercept form 




Slope is the rate of change of a line, which can be calculated by figuring out the change in y divided by the change in x, using the formula

When looking at a graph, you can pick two points on a graph and substitute their x- and y-values into that equation. On this graph, it's easier to choose points like 

Plugging in those values for