Electricity and Magnetism - MCAT Chemical and Physical Foundations of Biological Systems
Card 0 of 686
An electron is traveling at constant velocity directed to the the left through a magnetic field directed into the page as shown below.
Which way would the force vector on the electron due to the magnetic field be directed?
An electron is traveling at constant velocity directed to the the left through a magnetic field directed into the page as shown below.
Which way would the force vector on the electron due to the magnetic field be directed?
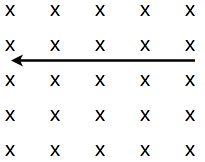
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
Compare your answer with the correct one above
What is the magnitude of force on a 
charge travelling at a constant velocity of 
through a perpendicular 
magnetic field?
What is the magnitude of force on a
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
Compare your answer with the correct one above
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become .
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become .
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
Compare your answer with the correct one above
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume 
is 90o.
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume
The force of a charge in a magnetic field is given by the equation 
. q is the charge, v is the velocity, and B is the magnetic field strength.
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation 
. I is the current, L is the length or the wire, and B is the magnetic field strength.
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation 
.
By manipulating the variables, we can generate the equation 
. None of the other answer choices can be derived from these equations.
The force of a charge in a magnetic field is given by the equation
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation
By manipulating the variables, we can generate the equation
Compare your answer with the correct one above
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
Compare your answer with the correct one above
The particle depicted above on the left has a charge of 
and a velocity 
going to the right. What will happen when the particle enters the magnetic field depicted?
The particle depicted above on the left has a charge of
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist 
clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist
Compare your answer with the correct one above
A circuit with two resistors (Resistor A and Resistor B) of equal resistance set up in parallel is attached to a battery with negligible internal resistance. Which of the following will occur if resistor B is removed?
(The wire of the circuit that resistor B is on will remain, however).
A circuit with two resistors (Resistor A and Resistor B) of equal resistance set up in parallel is attached to a battery with negligible internal resistance. Which of the following will occur if resistor B is removed?
(The wire of the circuit that resistor B is on will remain, however).
For this question we need to know that the voltage drop is equal through all paths of a parallel circuit; therefore we can realize that the voltage drop through both resistors are independent of each other. The current through resistor A will decrease with the removal of resistor B. Electrons want to travel through the path of least resistance.
For this question we need to know that the voltage drop is equal through all paths of a parallel circuit; therefore we can realize that the voltage drop through both resistors are independent of each other. The current through resistor A will decrease with the removal of resistor B. Electrons want to travel through the path of least resistance.
Compare your answer with the correct one above
Given that the resistance of resisitor R = 2Ω, what is the voltage drop across the 4 Ω resistor in the circuit shown above?
Given that the resistance of resisitor R = 2Ω, what is the voltage drop across the 4 Ω resistor in the circuit shown above?
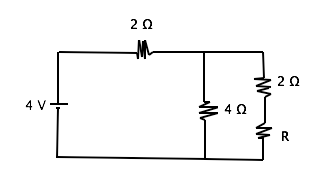
Given that resistor R = 2 Ω, we can see that the parallel aspect of the circuit has a resistance of 2 Ω as a whole, which means the total effective resistance of the circuit is 4 Ω. The potential difference drops 2V over the first resistor, then 2 V through the parallel aspect of the circuit. Potential difference, or voltage, drops through an equal amount in all branches of resistors in parallel. Therefore the remaining 2 V of potential difference is dropped by electrons moving through both branches of the parallel resistor, and the voltage drop through the 4 Ω resistor is 2V.
Given that resistor R = 2 Ω, we can see that the parallel aspect of the circuit has a resistance of 2 Ω as a whole, which means the total effective resistance of the circuit is 4 Ω. The potential difference drops 2V over the first resistor, then 2 V through the parallel aspect of the circuit. Potential difference, or voltage, drops through an equal amount in all branches of resistors in parallel. Therefore the remaining 2 V of potential difference is dropped by electrons moving through both branches of the parallel resistor, and the voltage drop through the 4 Ω resistor is 2V.
Compare your answer with the correct one above
What is the change in electrical potential energy for a charge of -2 µC moving through the circuit shown above?
What is the change in electrical potential energy for a charge of -2 µC moving through the circuit shown above?
Given that
V(q) = U
When V is voltage, U is electrical potential energy and q is charge, we can solve by plugging in 4 for V and -2 for q. Also, we must understand that the electric potential energy of a particle decreases as it moves from an area of higher energy to one of lower energy. For an electron, it has higher energy in the negative terminal of the battery than it does in when getting to the positive terminal.
Given that
V(q) = U
When V is voltage, U is electrical potential energy and q is charge, we can solve by plugging in 4 for V and -2 for q. Also, we must understand that the electric potential energy of a particle decreases as it moves from an area of higher energy to one of lower energy. For an electron, it has higher energy in the negative terminal of the battery than it does in when getting to the positive terminal.
Compare your answer with the correct one above
A capacitor attached to a 50 V battery aquires a charge of 10 C over a period of 5 seconds. How much energy is required to charge the capacitor?
A capacitor attached to a 50 V battery aquires a charge of 10 C over a period of 5 seconds. How much energy is required to charge the capacitor?
The power consumed by a capacitor is given by
After finding power, we can calculate the energy used as we are told that the capacitor took 5 seconds to charge. The units of power are watts which can be further broken down into joules per second. By multiplying the time taken to charge the capacitor by the power, we can find the total energy required to charge the capacitor.
The power consumed by a capacitor is given by
After finding power, we can calculate the energy used as we are told that the capacitor took 5 seconds to charge. The units of power are watts which can be further broken down into joules per second. By multiplying the time taken to charge the capacitor by the power, we can find the total energy required to charge the capacitor.
Compare your answer with the correct one above
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9 V battery with no internal resistance and three resistors as shown in the image below.
What is the voltage drop across the circuit?
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9 V battery with no internal resistance and three resistors as shown in the image below.
What is the voltage drop across the circuit?
This question asks us directly about one of Kirchhoff’s Loop Laws—more specifically the second law that states that the sum of the voltage around any loop must be equal to zero.
ΣVcircuit = 0V
Because the battery provides 9V, the voltage drop across the circuit must be 9V.
As an aside, the other Kirchhoff Law, the first law, states that current into a junction must equal the current that exits the junction, due to conservation of charge.
This question asks us directly about one of Kirchhoff’s Loop Laws—more specifically the second law that states that the sum of the voltage around any loop must be equal to zero.
ΣVcircuit = 0V
Because the battery provides 9V, the voltage drop across the circuit must be 9V.
As an aside, the other Kirchhoff Law, the first law, states that current into a junction must equal the current that exits the junction, due to conservation of charge.
Compare your answer with the correct one above
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.
What is the voltage drop across RA?
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.
What is the voltage drop across RA?
First, we need to determine the voltage drop across R1, and then we can subtract that from the 9V battery to determine the voltage drop across RA. Given that RA and R4 are in parallel, we know that the voltage drop across each is the same.
The voltage drop across R1 can be calculated using the Icircuit (all the current generated by the battery’s potential difference must pass through R1 because it is in direct series with the battery), and the resistance of the resistor.
I can be calculated by V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR allows us to find the current in the circuit.
V = IR
I = V/R = 9V/4Ω = 2.25 A
Plugging this value in, we can find the voltage drop across R1.
VR1 = IR = (2.25 A)(2Ω) = 4.5 V
Now we can determine the voltage drop across the parallel resistors by subtracting the voltage drop across R1 from the battery.
VA = 9V – 4.5V = 4.5V
Because RA and R4 are in parallel, the voltage drop across R4 is also 4.5V
First, we need to determine the voltage drop across R1, and then we can subtract that from the 9V battery to determine the voltage drop across RA. Given that RA and R4 are in parallel, we know that the voltage drop across each is the same.
The voltage drop across R1 can be calculated using the Icircuit (all the current generated by the battery’s potential difference must pass through R1 because it is in direct series with the battery), and the resistance of the resistor.
I can be calculated by V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR allows us to find the current in the circuit.
V = IR
I = V/R = 9V/4Ω = 2.25 A
Plugging this value in, we can find the voltage drop across R1.
VR1 = IR = (2.25 A)(2Ω) = 4.5 V
Now we can determine the voltage drop across the parallel resistors by subtracting the voltage drop across R1 from the battery.
VA = 9V – 4.5V = 4.5V
Because RA and R4 are in parallel, the voltage drop across R4 is also 4.5V
Compare your answer with the correct one above
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.
How much power does the circuit provide?
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.
How much power does the circuit provide?
This question asks us about the power of the circuit, meaning the amount of energy per unit time. The power equation is P = IV. V = IR can be substituted in to allow P to be calculated from a number of parameters.
P = IV = I2R = V2/R
To solve for P, we first need the current supplied by the battery.
We can use the formula V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR, we can solve for the current.
V = IR
I = V/R = 9V/4Ω = 2.25A
Now, we can use the current we calculated and the voltage that is dissipated across the circuit to calculate the power.
P = IV = (2.25 A)(9V) = 20.25W
This question asks us about the power of the circuit, meaning the amount of energy per unit time. The power equation is P = IV. V = IR can be substituted in to allow P to be calculated from a number of parameters.
P = IV = I2R = V2/R
To solve for P, we first need the current supplied by the battery.
We can use the formula V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR, we can solve for the current.
V = IR
I = V/R = 9V/4Ω = 2.25A
Now, we can use the current we calculated and the voltage that is dissipated across the circuit to calculate the power.
P = IV = (2.25 A)(9V) = 20.25W
Compare your answer with the correct one above
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.
Instead of assuming that the 9V battery has no internal resistance, what would the terminal potential of the battery be if it has an internal resistance of 
?
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.
Instead of assuming that the 9V battery has no internal resistance, what would the terminal potential of the battery be if it has an internal resistance of
Remember that internal resistance lowers the EMF of the battery. We need to calculate the voltage drop that would occur inside the battery, and then subtract that from the “stated” voltage to determine the terminal potential of the battery.
We first need the current supplied by the battery. We can use the formula V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR, we can find the current in the circuit.
V = IR
I = V/R = 9V/4Ω = 2.25A
Plugging in this value with the internal resistance of the battery gives us the voltage decrease.
V = IR = (2.25A)(0.9Ω) = 2.025V
Terminal Potential = 9V – 2.025V = 6.975V
As we can see, battery companies are interested in keeping the internal resistance of batteries at a minimum, because it lowers the overall terminal potential of the battery.
Remember that internal resistance lowers the EMF of the battery. We need to calculate the voltage drop that would occur inside the battery, and then subtract that from the “stated” voltage to determine the terminal potential of the battery.
We first need the current supplied by the battery. We can use the formula V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR, we can find the current in the circuit.
V = IR
I = V/R = 9V/4Ω = 2.25A
Plugging in this value with the internal resistance of the battery gives us the voltage decrease.
V = IR = (2.25A)(0.9Ω) = 2.025V
Terminal Potential = 9V – 2.025V = 6.975V
As we can see, battery companies are interested in keeping the internal resistance of batteries at a minimum, because it lowers the overall terminal potential of the battery.
Compare your answer with the correct one above
A circuit consists of a 
current passing through a 
resistor for 
. Find the heat generated.
A circuit consists of a
Ohm's Law states that 
. We are given the current and resistance, allowing us to solve for the voltage.
We also know that 
. Now that we have the voltage, we can solve for the power.
Finally, we know that 
. Using this, we can solve for the energy (or work) that is generated by the circuit.
Ohm's Law states that
We also know that
Finally, we know that
Compare your answer with the correct one above
A low resistance light bulb and a high resistance light bulb are connected in parallel with each other. This parallel combination is in series with a 
battery. Which bulb is brighter?
A low resistance light bulb and a high resistance light bulb are connected in parallel with each other. This parallel combination is in series with a
The brightness of each bulb depends on its power, or how much energy it dissipates per unit time. This can be calculated using the equation:
If the bulbs are in parallel with each other, the bulb with lower resistance will receive more current, since current will tend toward the path of least resistance. Current is squared in the power equation, so it is of greater importance in determining the power. The bulb with greater current and lower resistance will thus have more power and will shine more brightly.
The brightness of each bulb depends on its power, or how much energy it dissipates per unit time. This can be calculated using the equation:
If the bulbs are in parallel with each other, the bulb with lower resistance will receive more current, since current will tend toward the path of least resistance. Current is squared in the power equation, so it is of greater importance in determining the power. The bulb with greater current and lower resistance will thus have more power and will shine more brightly.
Compare your answer with the correct one above
What is the resistance in a wire carrying a voltage of 
and with a power of 
?
What is the resistance in a wire carrying a voltage of
The formula we can use here is the power formula that involved both resistance and voltage:
We are given the voltage and power, allowing us to solve for the resistance.
The formula we can use here is the power formula that involved both resistance and voltage:
We are given the voltage and power, allowing us to solve for the resistance.
Compare your answer with the correct one above
A 
current flows through a wire with a resistance of 
. Find the power generated by this current.
A
Electric power is expressed in a number of ways. We will need to use the relationship that involves current and resistance:
We are given the current and resistance, allowing us to calculate the power.
Electric power is expressed in a number of ways. We will need to use the relationship that involves current and resistance:
We are given the current and resistance, allowing us to calculate the power.
Compare your answer with the correct one above
Household voltage in the United States is 
, supplied by an alternating current (AC). What is the maximum voltage at the outlet?
Household voltage in the United States is
Alternative current (AC) voltage is governed by the RMS (root-mean square) voltage law. This means that the RMS voltage of the circuit will be 
, but the actual voltage will fluctuate between two values. These values are determined by the equation:
Using the values from our question, we can find the maximum voltage value.
Alternative current (AC) voltage is governed by the RMS (root-mean square) voltage law. This means that the RMS voltage of the circuit will be
Using the values from our question, we can find the maximum voltage value.
Compare your answer with the correct one above
Suppose you have a circuit with two resistors connected in parallel. The first resistor (resistor A) has a resistance of 
, whereas the second resistor (resistor B) has a resistance of 
. Which of the following is true regarding the power dissipated in the two resistors?
Suppose you have a circuit with two resistors connected in parallel. The first resistor (resistor A) has a resistance of
Recall that circuit elements (such as resistors) connected in parallel have the same potential difference; therefore, resistor A and resistor B must have the same potential difference. Since we have information about the potential difference and the resistance of the two resistors, it would be best to use the equation for power in terms of voltage and resistance.
Since the potential difference is constant for both resistors, the power will only depend on the resistance. The equation implies that the power decreases when resistance is high; therefore, resistor A will have lower power dissipation than resistor B because resistor A has the greater resistance.
Recall that circuit elements (such as resistors) connected in parallel have the same potential difference; therefore, resistor A and resistor B must have the same potential difference. Since we have information about the potential difference and the resistance of the two resistors, it would be best to use the equation for power in terms of voltage and resistance.
Since the potential difference is constant for both resistors, the power will only depend on the resistance. The equation implies that the power decreases when resistance is high; therefore, resistor A will have lower power dissipation than resistor B because resistor A has the greater resistance.
Compare your answer with the correct one above