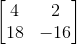To find the inverse of a matrix first look to verify that the matrix is square. If it is not square, it does not have an inverse. Next, you must find the determinant. If the determinant is 0, then the matrix does not have an inverse. The determinant for this matrix is ad-bc = 16, therefore it has an inverse. To find the inverse of a 2x2 matrix we first write it in augmented form.

First we will swap rows 1 and 2 next we will eliminate the first column by taking R2-2R1 , next we will divide R2/16 to set the second pivot. . Next we will eliminate the second column by taking R1-4R2. . Now that we have the identity matrix on the left, our answer is on the right. There is, however, an easier way to determine the inverse of a 2x2 matrix. The trick is to swap the numbers in spots a and d, put negatives in front of the numbers in spots b and c and then divide everything by the determinant. For this example, then divide by the determinant which is 16 and simplify.

The inverse of a square matrix - that is, a matrix with an equal number of rows and columns - if it exists, is equal in dimension to that matrix. Therefore, any inverse of a four-by-four matrix is itself a four-by-four matrix.

Only a square matrix - a matrix with an equal number of rows and columns - has an inverse. Therefore, a matrix with five rows and four columns cannot even have an inverse.

A matrix is involutory if . Since and are the same matrix, it immediately follows that is involutory.

The matrix is not square so it does not have an inverse.

A matrix is nonsingular - that is, it has an inverse - if and only if its determinant is nonzero. Also, the determinant of the product of two matrices is equal to the product of their individual determinants. Combining these ideas:

If either or , then it must hold that

.

Equivalently, if either or has no inverse, then has no inverse. Contrapositively, if has an inverse, it must hold that each of and has an inverse.

To simplify

we used the identities:

so we get

To prove a statement false, it suffices to find one case in which the statement does not hold. We show that

and

provide a counterexample.

A matrix is singular - that is, without an inverse - if and only if its determinant is equal to zero. The determinant of a two-by-two matrix is equal to the product of its upper left to lower right entries minus that of its upper right to lower left entries, so:

Both and are singular.

Now add the matrices by adding them term by term.

This is simply the two-by-two identity, which has an inverse - namely, itself.

The statement has been proved false by counterexample.

To find the inverse of a matrix first look to verify that the matrix is square. If it is not square, it does not have an inverse. Next, you must find the determinant. If the determinant is 0, then the matrix does not have an inverse. The determinant for this matrix is ad-bc = 9, therefore it has an inverse. To find the inverse of a 2x2 matrix we first write it in augmented form.

First we will divide R1/2 next we will eliminate the first column by taking R2-5R1 , next we will divide 9R2/2 to set the second pivot. . Next we will eliminate the second column by taking R1+1/2R2. . Now that we have the identity matrix on the left, our answer is on the right. There is, however, an easier way to determine the inverse of a 2x2 matrix. The trick is to swap the numbers in spots a and d, put negatives in front of the numbers in spots b and c and then divide everything by the determinant. For this example, then divide by the determinant which is 9 and simplify.

To find the inverse, first find the determinant. In this case, the determinant is

The inverse is found by multiplying