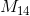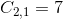Linear Algebra - The Determinant

Calculate the determinant of matrix A.

$A =\begin{bmatrix} 5&3 \ 6&4 \end{bmatrix}$

Not possible

Explanation

In order to find the determinant of a 2x2 matrix, compute $det A= a_{11}a_{22}-a_{12}a_{21}$ :

Consider the matrix

$A = \begin{bmatrix} -1&4 &1 \ -2& 3& 1\ 1&6 & 2 \end{bmatrix}$ .

Give cofactor $C_{33}$ of this matrix.

$C_{33}= 5$

$C_{33}=- 5$

$C_{33}= -11$

$C_{33}= 11$

$C_{33}= 0$

Explanation

The minor of a matrix $M_{mn}$ is the determinant of the matrix formed by striking out Row and Column . By definition, the corresponding cofactor $C_{mn}$ can be calculated from this minor using the formula

$C_{mn}= ( -1 )^{m+n} M_{mn}$

To find cofactor $C_{33}$ , we first find minor $M_{33}$ by striking out Row 3 and Column 3, as follows:

Minor

$M_{33}$ is equal to the determinant

$\begin{vmatrix} -1& 4\-2& 3 \end{vmatrix}$

which is found by taking the product of the upper left and lower right entries and subtracting that of the other two entries:

$M_{33} = (-1)(3)- 4 (-2) = -3 -(-8)= 5$

In the cofactor equation, set :

$C_{33}= ( -1 )^{3+3 } M_{33} = ( -1 )^{6 } \cdot 5 = 1 \cdot 5 = 5$

Let be a four-by-four matrix.

Cofactor $C_{13}$ must be equal to:

Minor $M_{13}$

The additive inverse of Minor $M_{14}$

The reciprocal of Minor $M_{14}$

The additive inverse of the reciprocal of Minor $M_{14}$

None of the other choices gives a correct response.

Explanation

$C_{mn}= ( -1 )^{m+n} M_{mn}$

Set ; the formula becomes

$C_{13}= ( -1 )^{1+3} M_{13}$

$C_{13}= ( -1 )^{ 4} M_{13}$

$C_{13}=1 \cdot M_{13}$

$C_{13}= M_{13}$ ,

making the quantities equal.

Consider the matrix

$A = \begin{bmatrix} -1&4 &1 \ -2& 3& 1\ 1&6 & 2 \end{bmatrix}$ .

Give cofactor $C_{2 3}$ of this matrix.

$C_{23} = 10$

$C_{23} = -10$

$C_{23} = 2$

$C_{23} = -2$

$C_{23} = 0$

Explanation

$C_{mn}= ( -1 )^{m+n} M_{mn}$

To find cofactor $C_{2 3}$ , we first find minor $M_{23}$ by striking out Row 2 and Column 3, as follows:

Minor

$M_{23}$ is equal to the determinant

$\begin{vmatrix} -1& 4\ 1& 6 \end{vmatrix}$

which is found by taking the product of the upper left and lower right entries and subtracting that of the other two entries:

$M_{23} = -1(6)- 1(4) = -6 - 4 = -10$

In the cofactor equation, set :

$C_{23}= ( -1 )^{2+3} M_{23}= ( -1 )^{5} (-10) = (-1)(-10) = 10$

Let be a five-by-five matrix.

Cofactor $C_{14}$ must be equal to:

The additive inverse of Minor $M_{14}$

Minor $M_{14}$

The additive inverse of the reciprocal of Minor $M_{14}$

The reciprocal of Minor $M_{14}$

None of the other choices gives a correct response.

Explanation

$C_{mn}= ( -1 )^{m+n} M_{mn}$

Set ; the formula becomes

$C_{14}= ( -1 )^{1+4} M_{14}$

$C_{14}= ( -1 )^{5} M_{14}$

$C_{14}=-1 \cdot M_{14}$

$C_{14}=- M_{14}$ .

Therefore, the cofactor $C_{14}$ must be equal to the opposite of the minor $M_{14}$ .

Consider the matrix

$A = \begin{bmatrix} 2& 3& -1\ -2& 1& 0\ 0& 1& 2 \end{bmatrix}$

Calculate the cofactor $C_{2,1}$ of this matrix.

$C_{2,1} = -7$

$C_{2,1} = 7$

$C_{2,1} = -5$

$C_{2,1} =5$

$C_{2,1} =0$

Explanation

The cofactor $C_{m, n}$ of a matrix , by definition, is equal to

$C_{m, n} = (-1)^{m + n} M_{m, n}$ ,

where $M_{m, n}$ is the minor of the matrix - the determinant of the matrix formed when Row and Column of are struck out. Therefore, we first find the minor $M_{2,1}$ of the matrix by striking out Row 2 and Column 1 of , as shown in the diagram below:

Minor

The minor is therefore equal to

$\begin{vmatrix} 3& -1\ 1& 2 \end{vmatrix}$

This is equal to the product of the upper-left and lower-right elements minus the product of the upper-right to lower-right elements, which is

$M_{2,1} = 3(2) - (-1)(1) = 6 - (-1) = 7$

Setting and in the definition of the cofactor, the formula becomes

$C_{2,1} = (-1)^{2 + 1} M_{2,1} = (-1)^{3} M_{2,1} = -1 \cdot M_{2,1}$ ,

$C_{2,1} = -1 \cdot 7 = -7$ .

Calculate the determinant of matrix A.

$A=\begin{bmatrix} 2&5 &4 &7 &1 \ 8& 6&11 & 3&9 \4 & 1&3 &0 &6 \ 7& 0&2 &9 &1 \end{bmatrix}$

Not possible

Explanation

It is not possible to calculate the determinant of this matrix because only square matrices (nxn) have determinants.

True or false: Square matrix is nilpotent if and only if $\det A = 0$ .

False

True

Explanation

A square matrix is nilpotent if, for some whole number , $A^{k} = O$ , the zero matrix of the same dimension as .

The determinant of the product of matrices is equal to the product of their determinants. It follows that if $A^{k} = O$ , $\left ( \det A \right )^{k} = \det O = 0$ , so $\det A = 0$ . Therefore, any nilpotent matrix must have determinant 0.

However, not all matrices with determinant 0 are nilpotent, as is proved by counterexample. Let

$A = \begin{bmatrix} 1 & 0 \ 0 & 0 \end{bmatrix}$

This matrix is diagonal, as its only nonzero entry is alone its main diagonal. To raise this to a power , simply raise all of the diagonal elements to the power of , and preserve the off-diagonal zeroes. It follows that for all $k \in \mathbb{N}$ ,

$A^{k} = \begin{bmatrix} 1^{k} & 0 \ 0 & 0 ^{k} \end{bmatrix} = \begin{bmatrix} 1 & 0 \ 0 & 0 \end{bmatrix} e O$

Also, the determinant of is $\det A = 1(0)- 0(0) = 0$ .

Since a non-nilpotent matrix with determinant zero exists, the biconditonal is false.

Calculate the determinant of $\begin{bmatrix} 5&-2 \ 1&3 \end{bmatrix}$ .

Explanation

By definition,

$\begin{vmatrix} a&b \ c&d \end{vmatrix}= a(d)-b(c)$ ,

therefore,

$\begin{vmatrix} 5&-2 \ 1&3 \end{vmatrix}= 5(3)-1(-2)= 17$ .

$A = \begin{bmatrix} 3&1 &0 \ 0&a &12 \ 1& 0 & a \end{bmatrix}$

is a singular matrix for what values of ?

$a=\pm 2i$

$a = \pm 2$

Explanation

A matrix is singular - without an inverse - if and only if its determinant is equal to 0.

One way to calculate the determinant of a three-by-three matrix is to add the products of the three diagonals going from upper-left to lower-right, then subtract the products of the three diagonals going from upper-right to lower left. From the diagram below:

Determinant