Transformations of Parabolic Functions
Help Questions
Algebra 2 › Transformations of Parabolic Functions
Consider the following two functions:

How is the function 











Explanation
The 


3 spaces right
3 spaces up
3 spaces down
3 spaces left
Explanation
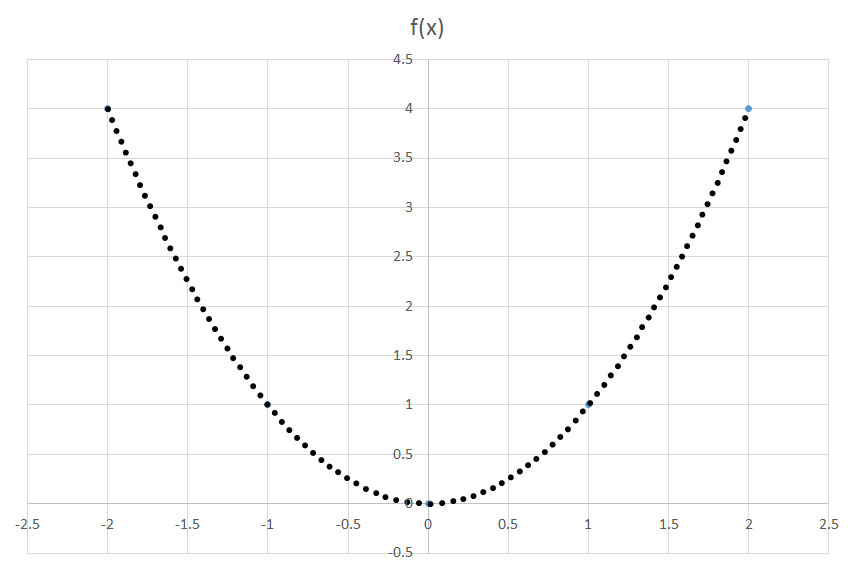
If the function 

Explanation
The function 



To translate along the y-axis, we use the function 

Describe the translation in
from the parent function

Down three units, right one unit
Up three units, right one unit
Up three units, left one unit
Down three units, left one unit
Explanation
Below is the standard equation for parabolas;
Therefore,

thus,
the translation from the parent function is down three units, right one unit.
Translate the parabola 
Explanation
To shift up 6 units, just add 6:
To shift to the right 3, subtract 3 from x:
First expand 
now this gives us:


Shift 
Explanation
Simplify the following equation by using the FOIL method with the binomial.
Simplify all terms in the parentheses.
Replace the term and simplify.
The equation in standard form is:
Since this parabola is shifted up one unit, add one to the y-intercept.
The answer is:
Given the parabola 
Explanation
Shifting up and down will result in a change in the y-intercept.
Add four to the equation.
Shifting the parabola to the left two units will change the inner term 


Replace the 

The new equation is:
Transform the following parabola: 
Shift up 

Explanation
When transforming paraboloas, to translate up, add to the equation (or add to the Y).
To translate to the left, add to the X.
Don't forget that if you add to the X, then since X is squared, the addition to X must also be squared.


Now adding the shift to the left we get:

Shift the parabola 
Explanation
Shifting this graph three units to the right means that the x-variable will need to be replaced with 
Use the FOIL method to simplify the binomial.
Simplify the right side.
The equation becomes:
The answer is:
Select the function that accuratley fits the graph shown.
Explanation
The parent function of a parabola is 

The original graph of a parabolic (quadratic) function has a vertex at (0,0) and shifts left or right by h units and up or down by k units.
.
This function then shifts 1 unit left, and 4 units down, and the negative in front of the squared term denotes a rotation over the x-axis.
Correct Answer:









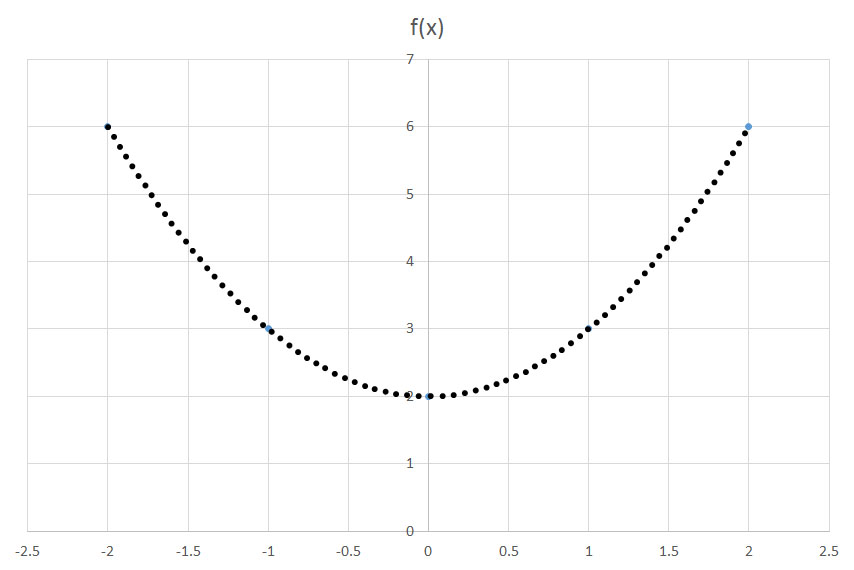































![y=2(x-2)^2+3+[4] =2(x-2)^2+7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/732331/gif.latex)























