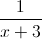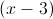Factor a two out in the numerator.

Factor the trinomial.

Factor the denominator.

Divide the terms.

The answer is:

To see what can be simplified, factor the quadratic equations.

Cancel out like terms:

Combine terms:

When we multiply expressions with exponents, we need to keep in mind some rules:

Multiplied variables add exponents.

Divided variables subtract exponents.

Variables raised to a power multiply exponents.

Therefore, when we mulitiply the two fractions, we obtain:

Our final answer is therefore

In the beginning, we can treat this as two separate problems, and factor the numerator and the denominator independently:

After we've factored them, we can put the factored equations back into the original problem:

From here, we can cancel the from the top and the bottom, leaving:

To simplify it is best to completely factor all polynomials:

Now cancel like terms:

Combine like terms:

Completely factor all polynomials:

Cancel like terms:

First factor the numerator. We need two numbers with a sum of 3 and a product of 2. The numbers 1 and 2 satisfy these conditions:

Now, look to see if there are any common factors that will cancel:

The in the numerator and denominator cancel, leaving .

The correct answer is . The numerator and denominator can both be factored to simpler terms:

The terms will cancel out. Leaving . While this is an answer choice, it can be simplified further. Factoring out a from the denominator will allow the terms to cancel out leaving .

a. Simplify the numerator and denominator separately by pulling out common factors.

b. Reduce if possible.

c. Factor the trinomial in the numerator.

d. Cancel common factors between the numerator and the denominator.

If we factors the denominator we get

Hence the rational expression becomes equal to

which is equal to