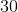Areas and Perimeters of Polygons
Help Questions
SSAT Upper Level Quantitative › Areas and Perimeters of Polygons
The area of a rectangle is 

Explanation
Let 


Since this is the length in feet, we multiply this by 12 to get the length in inches:
Find the area of a regular pentagon that has a side length of 

Explanation
To find the area of a regular polygon,
To find the perimeter of the pentagon,
For the given pentagon,
So then, to find the area of the pentagon,
Find the area of a regular hexagon that has side lengths of 
Explanation
Use the following formula to find the area of a regular hexagon:

Now, substitute in the length of the side into this equation.
The area of a rectangle is 

Explanation
Let 


Since this is the length in feet, we multiply this by 12 to get the length in inches:
Find the area of a regular hexagon that has side lengths of 
Explanation
Use the following formula to find the area of a regular hexagon:

Now, substitute in the length of the side into this equation.
A rectangle has the area of 80 square inches. The width of the rectangle is 2 inches longer that its height. Give the height of the rectangle.
Explanation
The area of a rectangle is given by multiplying the width times the height. That means:
where:


We know that: 

Now we should solve the equation for 
The equation has two answers, one positive 


A rectangle has the area of 80 square inches. The width of the rectangle is 2 inches longer that its height. Give the height of the rectangle.
Explanation
The area of a rectangle is given by multiplying the width times the height. That means:
where:


We know that: 

Now we should solve the equation for 
The equation has two answers, one positive 


Find the area of a regular pentagon that has a side length of 

Explanation
To find the area of a regular polygon,
To find the perimeter of the pentagon,
For the given pentagon,
So then, to find the area of the pentagon,
The area of a rectangle is 

Explanation
Let 


Since this is the length in feet, we multiply this by 12 to get the length in inches:
A rectangle has the area of 80 square inches. The width of the rectangle is 2 inches longer that its height. Give the height of the rectangle.
Explanation
The area of a rectangle is given by multiplying the width times the height. That means:
where:


We know that: 

Now we should solve the equation for 
The equation has two answers, one positive