How to find the part from the whole with percentage
Help Questions
PSAT Math › How to find the part from the whole with percentage
A total of 200,000 votes were cast for two opposing candidates. If the losing candidate received 40% of the vote, how many votes did the winning candidate receive?
120,000
80,000
100,000
50,000
Explanation
60% of 200,000 is 120,000
0.6 * 200,000 = 120,000
Your friend has 100 pounds of bacon and offers to share 45% of it with you. If you promised your mom 30% and your cousin 25% of your share, how many pounds of bacon do you end up with?
20.25 pounds
45 pounds
24.75 pounds
13.5 pounds
11.25 pounds
Explanation
Your share = 45% of 100 pounds of bacon = .45 * 100 = 45 pounds
For mom and cousin = 30% + 25% = 55%
Percent left for you = 100% - 55% = 45%
45% of 45 pounds = .45 * 45 = 20.25 pounds
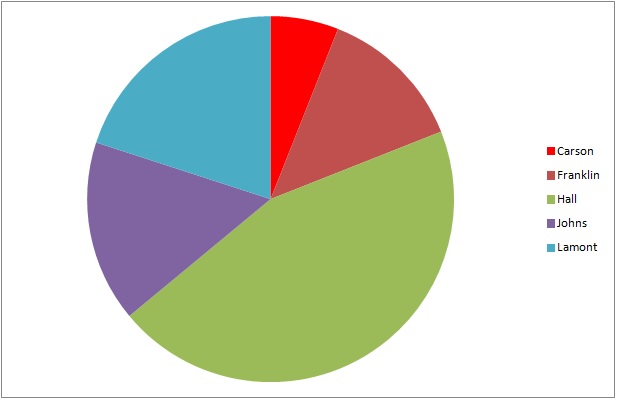
The above graph represents the results of a general election for two seats on the city council of Lincoln City. Frankllin and Hall are Democrats; Johns and Lamont are Republicans; Carson is an independent.
6,219 people voted for Republicans. Which of the following is the best estimate for the number of people who voted for Democrats?
Explanation
The two wedges that represent the Democratic candidates - green (Hall) and dark red (Franklin) - together make up about 60% of the circle. The two wedges that represent the Republican candidates - purple (Johns) and blue (Lamont) - make up about 35% of the circle. We can estimate the number of people who voted for a Democrat using a proportion statement:
10,660 is the best estimate.
Becky and Jason are running for class president, and each of the 30 students in the class voted. Becky received 60% of the votes. How many students voted for Jason?
12
15
18
21
Explanation
If Becky received 60% of the vote, Jason must have received 40% of the vote. 40% is equal to 0.40. By multiplying the number of votes times the percentage, we can calculate how many votes Jason received.
0.40 * 30 = 12.

The above graph represents the results of a general election for mayor of Washington City. Hall is a Republican; Johns is a Democrat; the other three are independents.
5,328 people voted for independent candidates. Which is the best estimate for the number of people who voted for Hall?
Explanation
The green wedge, which represents Hall, is about 45% of the circle. The three wedges representing independents Carson, Franklin, and Lamont - dark red, bright red, and turquoise, respectively - together comprise about 40% of the circle. We can set up, and solve for the unknown in, a proportion statement as follows:
The best estimate of the five is 6,000.
The pie chart illustrates how Carla allocates her money each week.
If she spends $200 on groceries each week, how much does she spend on rent?
1000
500
350
450
750
Explanation
1. 20% of Carla's whole budget is equal to $200. With this information, one can find Carla's weekly budget.
Set up the equation: 0.2b = 200 (b = budget).
b = 200/0.2 = 1000 = Carla's weekly budget
2. To find the amount Carla spends for rent, one needs to find what 35% of $1000 is.
0.35 x 1000 = 350
3. Because Carla spends 35% of her total budget on rent, she spends $350 on rent.
Three salesmen, Gor, Levon, and Raffi, competed to sell the highest number of cars in the month of August. A total of 250 cars were sold.
Gor sold 100 cars. Levon sold 62% of the remaining cars, and Raffi sold the rest.
How many cars did Raffi sell?
77
39
75
93
57
Explanation
We first subtract the 100 cars that Gor sold from the total of 250 sold. We are left with 150 cars, and we know that Levon sold 62% of them. 100% – 62% = 38%. Hence, Raffi sold 38% of 150 cars. 150 * 0.38 = 57
There are 



Explanation
If p is the number of pounds of cargo that is initially on the ship and m is the number of pounds of cargo that we transfer (or remove from the ship), we can find how many pounds of cargo are still on the ship after the transfer by the expression p – m. In order to model this as a percent, we would have to form a fraction, using the initial pounds of cargo, p, as the whole amount and p – m as the fractional part.
So,
we would get 
However, this problem asks us to find the percent, so we would simply multiply by 100
![\dpi{100} \small \left [\frac{100\left (p-m \right )}{p} \right ]%](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/18571/gif.latex)
A school is made up of 400 students. Each student must belong to one of the four clubs shown in the chart below. How many students are in chorus?

Explanation
You must first determine the percentage of the students in chorus. To do this, subtract the other percentages from 100: 100 – (35 + 29 + 24) = 12.
Therefore, 12% of the 400 students at this school attend chorus.
To determine the number of students in the chorus, multiply .12 (12%) by 400.
0.12(400) = 48
A container has ten liters of a twenty percent sucrose solution by volume. How many liters of the solution should be removed from the container and then replaced by the same volume of a forty percent sucrose solution, so that the final solution is ten liters of a twenty-five percent sucrose solution?
1.25
0.5
4
2
2.5
Explanation
The final solution is going to have a concentration of twenty-five percent and a volume of 10 liters. The amount of sucrose in the solution is equal to the concentration (expressed as a decimal) multiplied by the total volume. Therefore, the final solution will have 25% • 10 = 0.25 • 10 = 2.5 liters of sucrose.
Let x be the amount of the solution that is removed and then replaced by the forty percent solution. The amount of twenty percent solution that will remain will be equal to 10 – x, because the final solution will still have ten liters. (The amount removed is replaced with the same amount, so the final volume of the solution is the same.)
So we have to get 2.5 liters of sucrose from the twenty percent solution and the forty percent solution combined. The amount of sucrose we will get from the twenty percent solution equals the volume of the twenty percent solution (which we established will be 10 – x) multiplied by twenty percent as a decimal.
Amount of sucrose from 20% solution = 0.20 • (10 – x)
The amount of sucrose we get from the forty percent solution will equal the product of x and forty percent (since we defined x as the amount of forty percent solution).
Amount of sucrose from 40% solution = 0.40x
Now, we need to add the amount of sucrose from the 20% and the 40% solutions, and then set this equal to 2.5, because ultimately we will have 2.5 liters of sucrose in the solution. We can write the equation as follows and then solve for x:
0.20 • (10 – x) + 0.40x = 2.5
Here is a table that we can also use to summarize the information discussed above.
0.20 • (10 – x) + 0.40x = 2.5
Distribute.
2 – 0.2x + 0.4x = 2.5
Combine x terms.
2 + 0.2x = 2.5
Subtract 2 from both sides.
0.2x = 0.5
Divide both sides by 0.2.
x = 2.5 liters
The answer is 2.5 liters.
















![\dpi{100} \small \left [\frac{100\left (p-m \right )}{p} \right ]%](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/134/gif.latex)
![\dpi{100} \small \left [\frac{p}{100\left (p-m \right )} \right ]%](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/135/gif.latex)
![\dpi{100} \small \left [\frac{p-m}{100} \right ]%](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/136/gif.latex)
![\dpi{100} \small \left [\frac{100m}{p} \right ]%](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/137/gif.latex)
![\dpi{100} \small \left [\frac{100p}{m} \right ]%](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138/gif.latex)





