Plane Geometry
Help Questions
PSAT Math › Plane Geometry
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation
A regular seven sided polygon has a side length of 14”. What is the measurement of one of the interior angles of the polygon?
128.57 degrees
257.14 degrees
180 degrees
154.28 degrees
252 degrees
Explanation
The formula for of interior angles based on a polygon with a number of side n is:
Each Interior Angle = (n-2)*180/n
= (7-2)*180/7 = 128.57 degrees

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Explanation
The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 
Three angles of a hexagon measure 
This hexagon cannot exist.
Explanation
The sum of the degree measures of the angles of a (six-sided) hexagon, is
Let 


Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Explanation
The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 
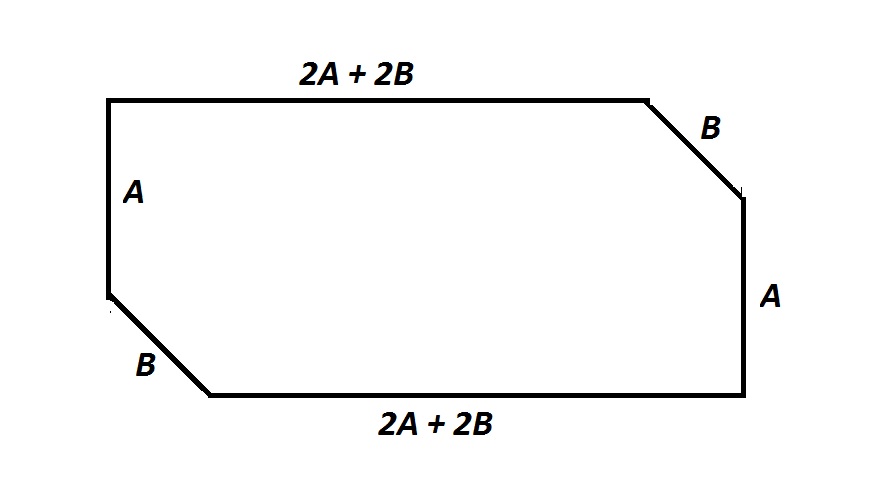
Note: Figure NOT drawn to scale.
The perimeter of the above figure is 600. The ratio of 



Explanation
The perimeter of the figure can be expressed in terms of the variables by adding:
Simplify and set 
Since the ratio of 



then
and we can substitute as follows:

Note: Figure NOT drawn to scale.
The perimeter of the above figure is 132. What is 
Explanation
The perimeter of the figure can be expressed in terms of the variables by adding:
Simplify and set 

Note: Figure NOT drawn to scale.
The perimeter of the above figure is 600. The ratio of 



Explanation
The perimeter of the figure can be expressed in terms of the variables by adding:
Simplify and set 
Since the ratio of 



then
and we can substitute as follows:

Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Explanation
The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Explanation
The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 



















































