Trigonometry - Solving Word Problems with Trigonometry

While waiting for your sister to finish her bungee jump, you decide to figure out how tall the platform she is jumping off is. You are standing feet from the base of the platform, and the angle of elevation from your position to the top of the platform is degrees. How many feet tall is the platform?

Explanation

You can draw the following right triangle using the information given by the question:

Since you want to find the height of the platform, you will need to use tangent.

$\tan 62=\frac{x}{200}$

Make sure to round to places after the decimal.

You need to build a diagonal support for the bleachers at the local sportsfield. The support needs to reach from the ground to the top of the bleacher. How the support should look is highlighted in blue below. The bleacher wall is 10 feet high and perpendicular to the ground. The owner would like the support to only stick out 3 feet from the bleacher at the bottom. What is the length of the support you need to build?

Screen shot 2020 08 27 at 1.35.40 pm

20 ft

10.44 ft

109 ft

11.32 ft

Explanation

It is important to recognize that the bleacher, the ground, and the support form a right triangle with the right angle formed by the intersection of the bleacher wall and the ground. We know the bottom of the support should only be 3ft from the bleacher wall on the ground and the bleacher wall is 10ft high. We will use the Pythagorean Theorem to solve for the length of the support, which is the hypotenuse of this right triangle. Our base of the triangle is 3 feet and the leg is 10 feet.

$a^{2}+b^{2}=c^{2}$

$3^{2}+10^{2}=c^{2}$

$109=c^{2}$

$\sqrt{109}=\sqrt{c^{2}}$

And so we need a support of 10.44 feet long.

When the angle of elevation of the sun is degrees, a flagpole casts a shadow that is feet long. In feet, how tall is the flagpole?

Explanation

You can draw the following right triangle from the information given by the question.

In order to find the height of the flagpole, you will need to use tangent.

$\tan 32=\frac{\text{height}}{10}$

$\text{height}=6.25$

Make sure to round to places after the decimal.

The flagpole is feet tall.

An airplane takes off from point and reaches its maximum altitude of 31,000 ft. The angle from the point of takeoff to the plane at maximum altitude is 55 degrees. What is the distance from point to where the plane reaches maximum altitude?

35,601 feet

31,000 feet

38,000 feet

37,844 feet

Explanation

We begin by drawing a picture. Let stand for where the plane reaches a maximum altitude of 31,000 ft. We can also assume that if we draw a line straight down from the plane that it will be perpendicular to the ground. This forms a right triangle.

Screen shot 2020 08 27 at 1.10.39 pm

Now we will use our knowledge of right triangles. We know the trigonometric identity, $\sin \left ( \theta \right )=\frac{opposite}{hypotenuse}$ . We can plug 55 in for our $\theta$ and 31,000 in for the opposite side. Solving for the hypotenuse is solving for the distance from the point of takeoff to the plane when it reaches maximum altitude.

$\sin \left ( \theta \right )=\frac{opposite}{hypotenuse}$

$\sin \left ( 55 \right )=\frac{31,000}h{}$

$h=\frac{31,000}{\sin \left ( 55 \right )}$

And so the distance from point to the plane at maximum altitude is 37,844 ft.

Two buildings with flat roofs are 80 feet apart. The shorter building is 55 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 32o. How high is the taller building?

49.6 feet

97.4 feet

104.6 feet

122.8 feet

129.6 feet

Explanation

To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle.

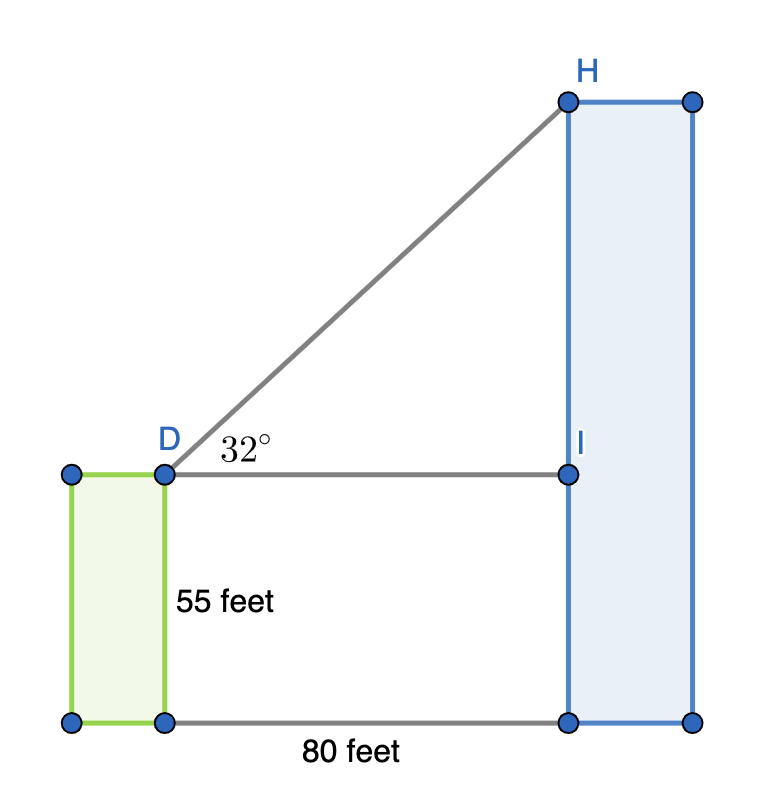
Screen shot 2020 07 13 at 5.58.09 pm

We are being asked to find the height of the taller building, but this diagram does not provide a triangle that has as one of its sides the entire height of the larger (rightmost and blue) building. However, we can instead find the distance $\overline{\rm HI}$ , and then add that to the 40 foot height of the shorter building to find the entire height of the taller building. Start by finding $\overline{\rm HI}$ :

$\tan32^\circ=\frac{\overline{\rm HI}}{80}$

$80\cdot \tan32^\circ=\overline{\rm HI}$

$80\cdot .62=\overline{\rm HI}$

$49.6=\overline{\rm HI}$

Remember that this is not the full height of the larger building. To find that, we need to add feet. Therefore, the taller building is 104.6 feet tall.

You are reading a billboard perpendicular to the ground walking downtown. You are standing about 500 ft from the base of the billboard and looking up at an angle of 67 degrees. About what height is the part of the billboard you are looking at standing at? Round to the nearest whole number.

1,178 feet

500 feet

5,325 feet

2,367 feet

Explanation

We begin by drawing a picture. Let point be where your eyes are looking on the billboard and point be where you are standing on the ground.

We must solve for the height of the billboard. We have information of the adjacent side of the right triangle formed and we wish to know the height, which will be the opposite side from you. Using trigonometric identities, we will use . We can plug in 500 ft for our adjacent side and 67 degrees for our .

And the height of the section of the billboard you are looking at is 1,178 ft above the ground.

Two buildings with flat roofs are 50 feet apart. The shorter building is 40 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 48o. How high is the taller building?

40 feet

55.5 feet

73.5 feet

77.2 feet

95.5 feet

Explanation

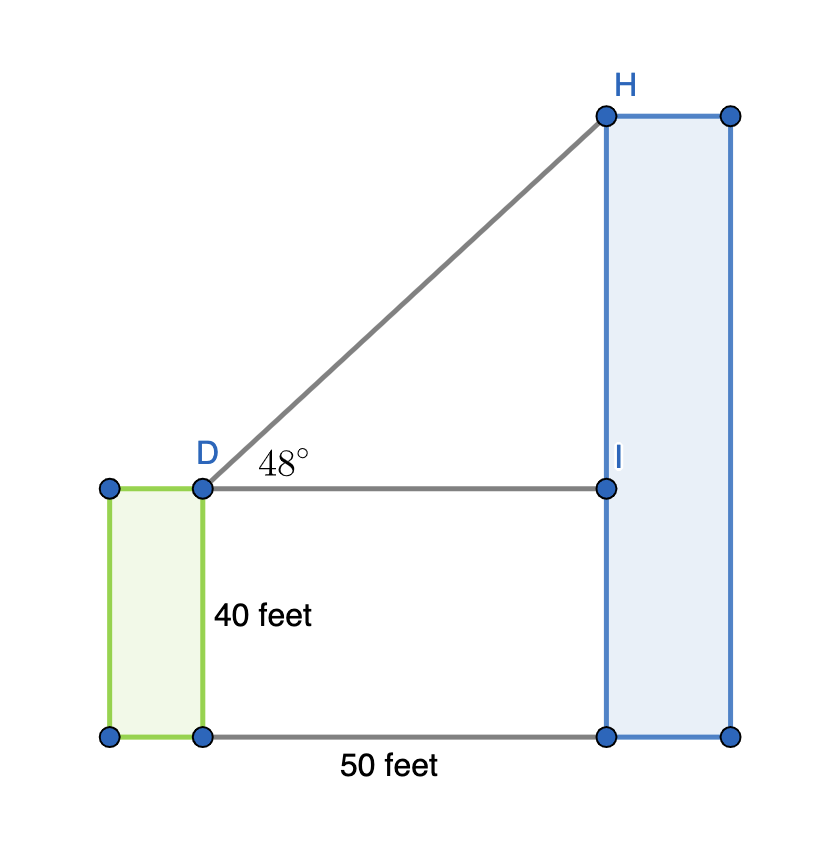
Screen shot 2020 07 13 at 5.56.45 pm

$\tan48^\circ=\frac{\overline{\rm HI}}{50}$

$50\cdot \tan48^\circ=\overline{\rm HI}$

$50\cdot 1.11=\overline{\rm HI}$

$55.5=\overline{\rm HI}$

Remember that this is not the full height of the larger building. To find that, we need to add feet. Therefore, the taller building is 95.5 feet tall.

Two buildings with flat roofs are 330 feet apart. The shorter building is 31.4 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 61.4o. How high is the taller building?

189.4 feet

321.13 feet

603.9 feet

635.3 feet

933.9 feet

Explanation

Screen shot 2020 07 13 at 6.00.03 pm

$\tan61.4^\circ=\frac{\overline{\rm HI}}{330}$

$330\cdot \tan61.4^\circ=\overline{\rm HI}$

$330\cdot 1.83=\overline{\rm HI}$

$603.9=\overline{\rm HI}$

Remember that this is not the full height of the larger building. To find that, we need to add feet. Therefore, the taller building is 635.3 feet tall.

You have a shadow that measures 66cm from your feet. You are 60cm tall. What is the sun’s angle of elevation? Round to the nearest degree.

$48^\circ$

$42^\circ$

$36^\circ$

$54^\circ$

Explanation

The important thing to note for this problem is that we are working with similar triangles. Your shadow forms a right triangle with its three points being your feet, the top of your head, and the top of your shadow’s head. We have enough information to find the angle of your head’s elevation to your shadow on the ground. Just like your shadow forms a right triangle to your body, a similar right triangle will also be formed to the sun’s altitude. We know that this triangle is similar because it shares the angle opposite your body and it shares a right angle, so it’s third angle must also be equal. Since it shares the angle opposite your body, we must only solve for the angle of your head’s elevation and it will be the same as the sun’s elevation.

We do this by using . We can plug in 60cm for the opposite since that is your height, and 66cm for the adjacent since that is the length of the shadow. We are solving for .

And so the sun is at an elevation of 48 degrees.

From the top of a lighthouse that sits 105 meters above the sea, the angle of depression of a boat is 19o. How far from the boat is the top of the lighthouse?

36.15 meters

110.53 meters

318.18 meters

423.18 meters

Explanation

To solve this problem, we need to create a diagram, but in order to create that diagram, we need to understand the vocabulary that is being used in this question. The following diagram clarifies the difference between an angle of depression (an angle that looks downward; relevant to our problem) and the angle of elevation (an angle that looks upward; relevant to other problems, but not this specific one.) Imagine that the top of the blue altitude line is the top of the lighthouse, the green line labelled GroundHorizon is sea level, and point B is where the boat is.

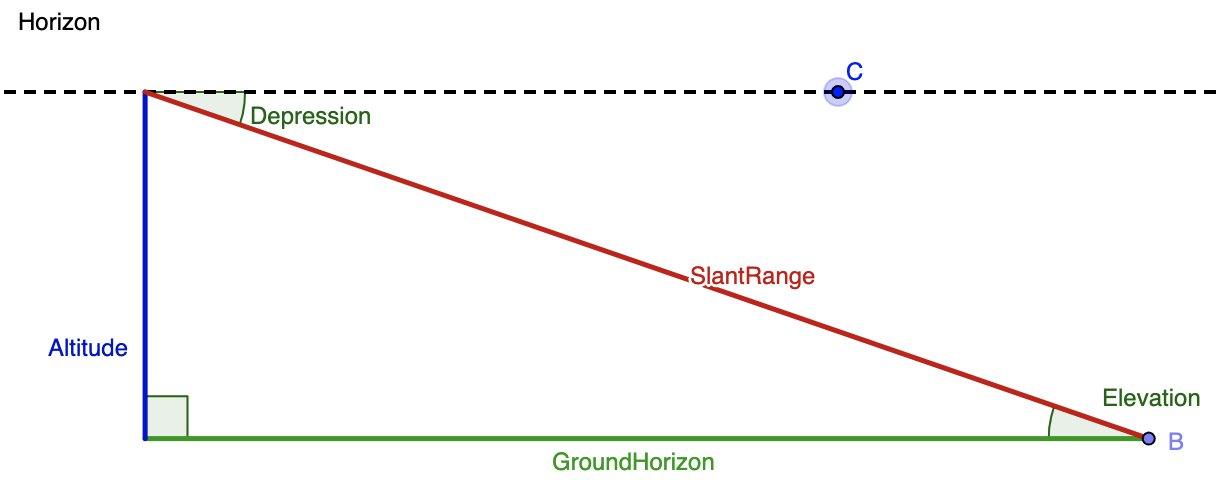
Screen shot 2020 07 13 at 3.07.05 pm

Merging together the given info and this diagram, we know that the angle of depression is 19o and and the altitude (blue line) is 105 meters. While the blue line is drawn on the left hand side in the diagram, we can assume is it is the same as the right hand side. Next, we need to think of the trig function that relates the given angle, the given side, and the side we want to solve for. The altitude or blue line is opposite the known angle, and we want to find the distance between the boat (point B) and the top of the lighthouse. That means that we want to determine the length of the hypotenuse, or red line labelled SlantRange. The sine function relates opposite and hypotenuse, so we'll use that here. We get:

$\sin 19^\circ=\frac{105}{d}$ (where d is the distance between the top of the lighthouse and the boat)