Angle Applications - Trigonometry

Card 1 of 96

0

Didn't Know

0

Didn't Know

Knew It

0

1 of 2019 left

Question

True or False: You are given the central angle measure but no other information, you are able to solve for the arc length.

Tap to reveal answer

Answer

We do not have enough information to solve for the arc length. We know that the measure of the arc is equal to the central angle and that the measure of the arc is $\theta = $\frac{r}{l_A}$$ but we still have two unknowns with no method to solve for them.

← Didn't Know|Knew It →

Question

Which is true of the relationship between the arc measure and the central angle as shown below?

Tap to reveal answer

Answer

Every arc has a measure that is equal to the measure of the central angle that creates the arc. This is because the measure of the angle determines the distance around the circumference that the arc makes.

← Didn't Know|Knew It →

Question

Which of the following is the correct formula for finding arc length?

Tap to reveal answer

Answer

The circumference of an entire circle is $2\pi r$ . When considering the length of an arc, the angle is less than $2\pi$ denoted by angle $\theta$ . So the formula for finding the length of an arc is replacing the angle of an entire circle, $2\pi$ , with the angle that forms the arc, $\theta$ . This gives us the formula $l_A = \theta r$ .

← Didn't Know|Knew It →

Question

Which of the following is the correct arc length formed by the angle $\frac{\pi}{3}$ of a circle whose radius is a length of 5?

Tap to reveal answer

Answer

We must use the formula for finding arc length $l_A = \theta r$ . We have been given all the information needed to just plug into the formula.

$l_A = \theta r$

$l_A = $\frac{\pi}{3}$ 5$

$l_A = $\frac{5\pi}{3}$$

← Didn't Know|Knew It →

Question

Which of the following is the correct arc length formed by an angle with measure 30 degrees of a circle whose radius is a length of 3?

Tap to reveal answer

Answer

First, we are given our angle measure in degrees and we must convert to radians to be able to use our arc length formula.

$30 $\frac{\pi}{180}$ = $\frac{\pi}{6}$$

Now we are able to plug the radius length and the angle measure into our formula and solve for the arc length.

$l_A = $\frac{\pi}{6}$ 3$

$l_A = $\frac{3\pi}{6}$$

$l_A = $\frac{\pi}{2}$$

← Didn't Know|Knew It →

Question

What is the measure of the angle that forms an arc with length 2.33 of a circle who has radius 4? Round to the second decimal place.

Tap to reveal answer

Answer

We must use the formula for finding arc length to solve for the measure of the angle, $\theta$ . The formula is $l_A = \theta r$ .

$l_A = \theta r$

$2.33 = \theta 4$

$0.58 = \theta$

← Didn't Know|Knew It →

Question

An arc has a measure of $\frac{\pi}{4}$ and a diameter of 7, what is the measure of the central angle?

Tap to reveal answer

Answer

Notice the question gave you the measure of the arc, NOT the arc length. The measure of an arc is equal to the measure of the central angle that forms the arc. We do not even need to use our formula for this one, just the fact that the central angle is equal to the measure of the arc that it forms.

← Didn't Know|Knew It →

Question

You know that the central angle of a sector is $\frac{3\pi}{2}$ and the sector area is $\frac{7\pi}{4}$ , what is the arc length? Round to two decimals.

Tap to reveal answer

Answer

The formula to find the area of a sector is $A = $\frac{\theta}{2}$ $r^2$$ . The piece of information we are missing to solve for arc length is the radius, so we will use the formula for finding the area of a sector to solve for radius, allowing us to solve for the arc length.

$A = $\frac{\theta}{2}$ $r^2$$

$\frac{7\pi}{4}$ = $($\frac{3\pi}$){2}($\frac{1}{2}$)r^2$

$\frac{7\pi}{4}$ = ($\frac{3\pi}{4}$ $r^2$

$\frac{7\pi}{3}$ = $r^2$

$$\sqrt{\frac{7\pi}{3}$} = r$

Now we can plug this into our formula to solve for arc length

$l_A = \theta r$

$l_A = $\frac{3\pi}{2}$ (2.707)$

← Didn't Know|Knew It →

Question

Which is true of the relationship between the arc measure and the central angle as shown below?

Tap to reveal answer

Answer

Every arc has a measure that is equal to the measure of the central angle that creates the arc. This is because the measure of the angle determines the distance around the circumference that the arc makes.

← Didn't Know|Knew It →

Question

Which of the following is the correct formula for finding arc length?

Tap to reveal answer

Answer

The circumference of an entire circle is $2\pi r$ . When considering the length of an arc, the angle is less than $2\pi$ denoted by angle $\theta$ . So the formula for finding the length of an arc is replacing the angle of an entire circle, $2\pi$ , with the angle that forms the arc, $\theta$ . This gives us the formula $l_A = \theta r$ .

← Didn't Know|Knew It →

Question

Which of the following is the correct arc length formed by the angle $\frac{\pi}{3}$ of a circle whose radius is a length of 5?

Tap to reveal answer

Answer

We must use the formula for finding arc length $l_A = \theta r$ . We have been given all the information needed to just plug into the formula.

$l_A = \theta r$

$l_A = $\frac{\pi}{3}$ 5$

$l_A = $\frac{5\pi}{3}$$

← Didn't Know|Knew It →

Question

Which of the following is the correct arc length formed by an angle with measure 30 degrees of a circle whose radius is a length of 3?

Tap to reveal answer

Answer

First, we are given our angle measure in degrees and we must convert to radians to be able to use our arc length formula.

$30 $\frac{\pi}{180}$ = $\frac{\pi}{6}$$

Now we are able to plug the radius length and the angle measure into our formula and solve for the arc length.

$l_A = $\frac{\pi}{6}$ 3$

$l_A = $\frac{3\pi}{6}$$

$l_A = $\frac{\pi}{2}$$

← Didn't Know|Knew It →

Question

What is the measure of the angle that forms an arc with length 2.33 of a circle who has radius 4? Round to the second decimal place.

Tap to reveal answer

Answer

We must use the formula for finding arc length to solve for the measure of the angle, $\theta$ . The formula is $l_A = \theta r$ .

$l_A = \theta r$

$2.33 = \theta 4$

$0.58 = \theta$

← Didn't Know|Knew It →

Question

An arc has a measure of $\frac{\pi}{4}$ and a diameter of 7, what is the measure of the central angle?

Tap to reveal answer

Answer

Notice the question gave you the measure of the arc, NOT the arc length. The measure of an arc is equal to the measure of the central angle that forms the arc. We do not even need to use our formula for this one, just the fact that the central angle is equal to the measure of the arc that it forms.

← Didn't Know|Knew It →

Question

True or False: You are given the central angle measure but no other information, you are able to solve for the arc length.

Tap to reveal answer

Answer

We do not have enough information to solve for the arc length. We know that the measure of the arc is equal to the central angle and that the measure of the arc is $\theta = $\frac{r}{l_A}$$ but we still have two unknowns with no method to solve for them.

← Didn't Know|Knew It →

Question

You know that the central angle of a sector is $\frac{3\pi}{2}$ and the sector area is $\frac{7\pi}{4}$ , what is the arc length? Round to two decimals.

Tap to reveal answer

Answer

The formula to find the area of a sector is $A = $\frac{\theta}{2}$ $r^2$$ . The piece of information we are missing to solve for arc length is the radius, so we will use the formula for finding the area of a sector to solve for radius, allowing us to solve for the arc length.

$A = $\frac{\theta}{2}$ $r^2$$

$\frac{7\pi}{4}$ = $($\frac{3\pi}$){2}($\frac{1}{2}$)r^2$

$\frac{7\pi}{4}$ = ($\frac{3\pi}{4}$ $r^2$

$\frac{7\pi}{3}$ = $r^2$

$$\sqrt{\frac{7\pi}{3}$} = r$

Now we can plug this into our formula to solve for arc length

$l_A = \theta r$

$l_A = $\frac{3\pi}{2}$ (2.707)$

← Didn't Know|Knew It →

Question

Which of the following is the definition for a sector of a circle?

Tap to reveal answer

Answer

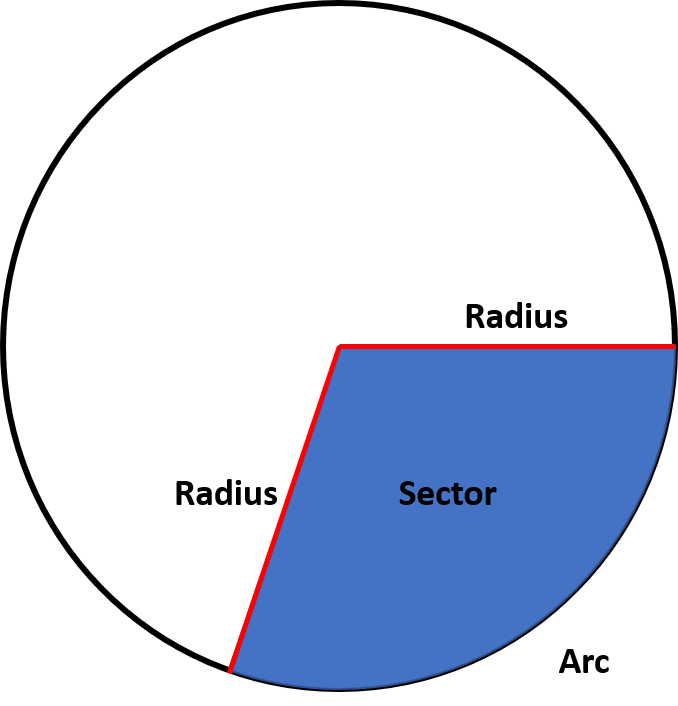
Below is an illustration of a sector of a circle. A sector is the area of a circle which has been enclosed by two radii and the arc between them. A sector is not to be confused with a segment of a circle. A segment is when the area enclosed by the chord of a circle and the arc of the chord.

← Didn't Know|Knew It →

Question

Which of the following is the formula for the area of a sector?

Tap to reveal answer

Answer

When thinking about how to derive the formula for a sector, we must consider the angle of an entire circle. The angle of an entire circle, 360 degrees, is $2\pi$ and we know the area of a circle is $\pi $r^2$$ .

When considering a sector, this is only a portion of the entire circle, so it is a particular $\theta$ out of the entire $2\pi$ . We can plug this into our area for a circle and it will simplify to the area of a sector.

$\frac{\theta}{2\pi}$\pi $r^2$

$\frac{\theta}{2}$ $r^2$

← Didn't Know|Knew It →

Question

If a circle has a sector with an angle of $\theta = 60$ and diameter of 4, what is the area of the sector?

Tap to reveal answer

Answer

It is always best to draw a picture in order to visualize the problem you are trying to solve. The figure below shows the sector we are trying to find the area of.

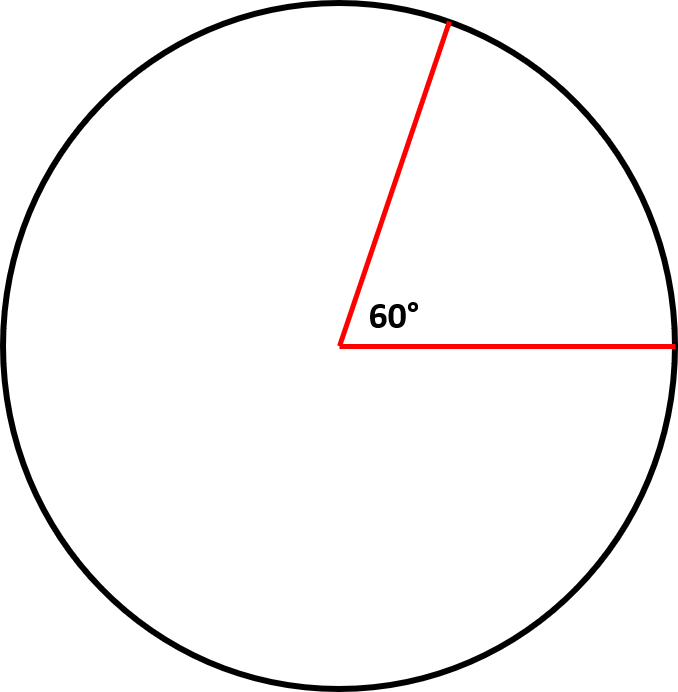
We know that the formula to find the area of a sector is $A = $\frac{\theta}{2}$ $r^2$$ . From the information given above we know that the diameter is 4. Since we only need the radius for our formula we divide the diameter by 2 to get the radius length. The radius has a length of 2. We also know that we have our angle measure in degrees and must convert it to radians. We use the conversion formula $degrees $\frac{\pi}{180}$ = radians$ .

$60 $\frac{\pi}{180}$ = $\frac{\pi}{3}$$

Now we can plug everything into our formula and solve.

$A = $$\frac{\theta}{2}$r^2$$

$A = $\frac{\pi}{3}$$\frac{1}{2}$ $2^2$$

$A = $\frac{\pi}{6}${4}$

$A = $\frac{2\pi}{3}$$

← Didn't Know|Knew It →

Question

True or False: The formula to find the area of a sector only works for acute angles.

Tap to reveal answer

Answer

This is not true. Even obtuse angles are less than $2\pi$ so this formula will still work. We can demonstrate this using the sector below. The radius of the circle is 6 and the obtuse angle is 330 degrees.

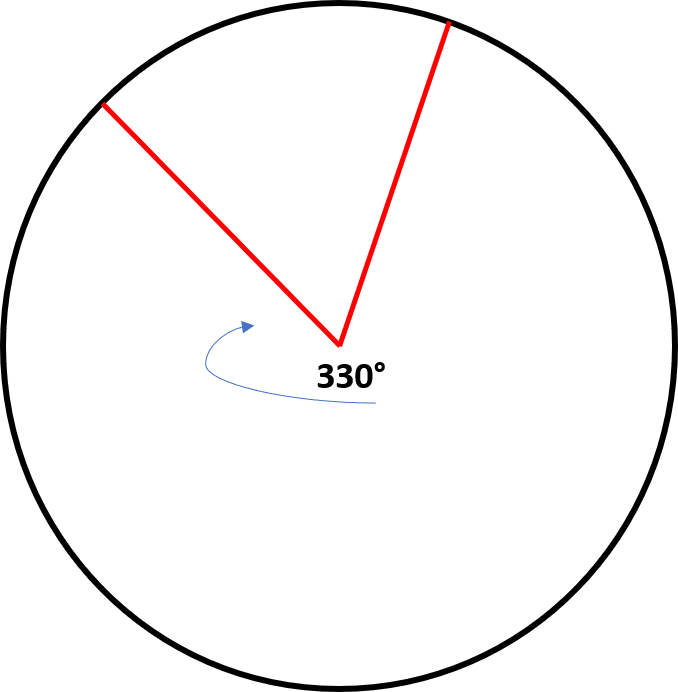
Converting 330 degrees to radians:

$330 $\frac{\pi}{180}$ = $\frac{11\pi}{6}$$

We can now plug this into our formula

$A = $\frac{\theta}{2}$ $r^2$$

$A = $\frac{11\pi}{6}$$\frac{1}{2}$ $6^2$$

$A = $\frac{11\pi}{12}$ 36$

$A = $\frac{396\pi}{12}$$

$A = 33\pi$

Now we can confirm this to be true by computing the area of the sector formed by the

area leftover formed by the acute angle, 30 degrees. To do this we will first find the total

area of the circle and then subtract the area of the sector formed by the acute angle. This should be equal to the area of the larger vector if our formula works for all angles because the sum of both sectors should be the total area of the circle.

To find the area of the circle:

$\pi $r^2$$

$36\pi$

To find the area of the smaller sector (note, 30 degrees in radians is $\frac{\pi}{6}$ :

$A = $\frac{\theta}{2}$ $r^2$$

$A = $\frac{\pi}{6}$$\frac{1}{2}$ $6^2$$

$A = $\frac{\pi}{12}$ 36$

$A = 3\pi$

Clearly, the total area of the circle minus the area of the small sector is equal to the area

of the larger circle, therefore this formula works for all angles less than $2\pi$

$36\pi - 3\pi = 33\pi$

← Didn't Know|Knew It →

0

Knew It