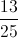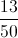SSAT Middle Level Quantitative - How to find the probability of an outcome

Dave has a sock drawer with 8 blue and 10 black socks.

If Dave pulls out one black sock, what is the probability that the next sock he pulls out of the drawer is also black?

9 out of 17

5 out of 9

10 out of 17

1 out of 2

4 out of 9

Explanation

Since the first sock that Dave pulls out is black, there are 17 remaining socks in the drawer, 8 blue and 9 black. The probability that Dave will choose another black is sock is therefore 9 out of 17.

A pair of fair dice are rolled. What is the probability that the sum will be a multiple of 4?

$\frac{1}{4}$

$\frac{1}{3}$

$\frac{5}{18}$

$\frac{3}{10}$

$\frac{11}{36}$

Explanation

There are three possible multiples of 4 that can come out: 4, 8, and 12. There are 36 equally probable outcomes; the following will result in a multiple of 4:

These are 9 outcomes out of 36, making the probability $\frac{9}{36} = \frac{1}{4}$

A pair of fair dice are rolled. What is the probability that the sum will be a multiple of 3?

$\frac{1}{3}$

$\frac{1}{4}$

$\frac{5}{18}$

$\frac{3}{10}$

$\frac{11}{36}$

Explanation

There are four possible multiples of 3 that can come out: 3,6,9, and 12. There are 36 equally probable outcomes; the following will result in a multiple of 3:

These are 12 outcomes out of 36, making the probability $\frac{12}{36} = \frac{1}{3}$

If Mark flips a coin and then rolls a die, what are the odds that the coin will be heads and that the die will land on a multiple of 3?

$\frac{1}{6}$

$\frac{1}{3}$

$\frac{1}{12}$

$\frac{1}{4}$

Explanation

If Mark flips a coin, the chance that it will land on heads is $\frac{1}{2}$ . On a die, there are 2 out of 6 numbers that are a multiple of 3 (3 and 6); therefore, there is a $\frac{1}{3}$ chance that the dice will be a multiple of 3.

The probability that the coin will land on heads and that the dice will be a multiple of 3 is:

$\frac{1}{2}*\frac{1}{3}=\frac{1}{6}$

A large box contains some balls, each of which is marked with a number; one ball is marked with a "1", two balls are marked with a "2". and so forth up to ten balls with a "10". A blank ball is also included.

Give the probability that a ball drawn at random will NOT be an odd-numbered ball.

$\frac{31}{56}$

$\frac{15}{28}$

$\frac{31}{55}$

$\frac{6}{11}$

Explanation

The number of balls in the box is

;

The number of odd-numbered balls is

Therefore, there are balls that are not marked with an odd number, making the probability that one of these will be drawn $\frac{31}{56}$ .

Lisa and Fred were flipping a quarter and recording whether it was heads or tails. What is the probability they flip a quarter and it lands on heads, heads, tails, heads, tails? (H,H,T,H,T)

$\frac{1}{32}$

$\frac{1}{16}$

$\frac{1}{10}$

$\frac{1}{5}$

$\frac{1}{2}$

Explanation

There are two possibilities every time you flip a coin and only one outcome. Therefore the probability for flipping either heads or tails each time is $\frac{1}{2}$ . When you have multiple trials in a row you multiply the probabilities of each outcome by each other.

$\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{32}$

In a bag of marbles, there are blue marbles, red marbles, and green marbles. What is the probability of drawing two blue marbles in a row?

$\frac{1}{15}$

$\frac{1}{9}$

$\frac{3}{10}$

$\frac{4}{90}$

Explanation

The probability of drawing a blue marble on the first try is $\frac{3}{10}$ , since there are blue marbles out of a total of marbles. The probability of drawing a second blue marble is $\frac{2}{9}$ , since now there are blue marbles remaining out of a total of remaining marbles. The probability of drawing two blue marbles in a row is the product of the individual probabilities: $\frac{3}{10}\cdot\frac{2}{9}=\frac{6}{90}=\frac{1}{15}$ .

The red jacks are removed from a standard deck of fifty-two cards. What is the probability that a card randomly drawn from that modified deck will be black?

$\frac{13}{25}$

$\frac{1}{2}$

$\frac{12}{25}$

$\frac{1}{4}$

$\frac{13}{50}$

Explanation

The removal of two red jacks - and no black cards - results in there being fifty cards, twenty-six of them black. Therefore, the probability of a randomly drawn card being black is $\frac{26}{50} = \frac{13}{25}$ .

A large box contains some balls, each of which is marked with a letter of the alphabet. Each vowel is represented by three balls, one red and two blue; each consonant is represented by one ball, which is red. Give the probability that a randomly drawn ball will be blue.

Note: For purposes of this question, "Y" is considered a consonant.

$\frac{5}{18}$

$\frac{13}{18}$

$\frac{10}{31}$

$\frac{21}{31}$

Explanation

Each of the 26 letters is represented by one red ball; in addition, each of the five vowels is represented by two blue balls for a total of $5 \times 2 = 10$ blue balls. The total number of balls is

The probability that a random draw will result in a blue ball being selected is

$\frac{10}{36} = \frac{5}{18}$ .

All of the clubs are removed from a standard fifty-two-card deck. Two cards are then dealt without replacement. What is the probability that both cards will be red?

$\frac{25}{57}$

$\frac{2}{3}$

$\frac{4}{9}$

$\frac{1}{4}$

$\frac{25}{51}$

Explanation

Wihtout the clubs, the deck comprises 39 cards, 26 of which are red.

The probability that the first card will be red will be $\frac{26}{39} = \frac{2}{3}$ . The probability that the second will then also be red will be $\frac{25}{38}$ . Multiply the probabilities, and result is $\frac{2}{3} \cdot \frac{25}{38} =\frac{1}{3} \cdot \frac{25}{19} = \frac{25}{57}$

How to find the probability of an outcome

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation