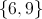Venn Diagrams
Help Questions
PSAT Math › Venn Diagrams


Find 
Explanation
The intersection of two sets contains every element that is present in both sets, so 


Find 
Explanation
The intersection of two sets contains every element that is present in both sets, so 
100 students are in the 10th grade class. 30 are swimmers, 40 are runners, and 20 are swimmers and runners. What is the probability that a student is a swimmer OR a runner?
1/2
1/3
1/5
1/4
2/3
Explanation
The formula for intersection is P(a or b) = P(a) + P(b) – P(a and b).
Now, 30 students out of 100 swim, so P(swim) = 30/100 = 3/10.
40 students run out of 100, so P(run) = 40/100 = 4/10. Notice how we are keeping 10 as the common denominator even though we could simplify this further. Keeping all of the fractions similar will make the addition and subtraction easier later on.
Finally, 20 students swim AND run, so P(swim AND run) = 20/100 = 2/10. (Again, we keep this as 2/10 instead of 1/5 so that we can combine the three fractions more easily.)
P(swim OR run) = P(swim) + P(run) – P(swim and run)
= 3/10 + 4/10 – 2/10 = 5/10 = 1/2.
100 students are in the 10th grade class. 30 are swimmers, 40 are runners, and 20 are swimmers and runners. What is the probability that a student is a swimmer OR a runner?
1/2
1/3
1/5
1/4
2/3
Explanation
The formula for intersection is P(a or b) = P(a) + P(b) – P(a and b).
Now, 30 students out of 100 swim, so P(swim) = 30/100 = 3/10.
40 students run out of 100, so P(run) = 40/100 = 4/10. Notice how we are keeping 10 as the common denominator even though we could simplify this further. Keeping all of the fractions similar will make the addition and subtraction easier later on.
Finally, 20 students swim AND run, so P(swim AND run) = 20/100 = 2/10. (Again, we keep this as 2/10 instead of 1/5 so that we can combine the three fractions more easily.)
P(swim OR run) = P(swim) + P(run) – P(swim and run)
= 3/10 + 4/10 – 2/10 = 5/10 = 1/2.
We have two sports clubs offered to a class of 100 students. 70 students joined the basketball club, 40 students joined the swimming club, and 10 students joined neither. How many students joined both the swimming club and the basketball club?
Explanation
The idea is to draw a Venn Diagram and find the intersection. We have one circle of 70 and another with 40. When we add the two circles plus the 10 students who joined neither, we should get 100 students. However, when adding the two circles, we are adding the intersections twice, therefore we need to subtract the intersection once.
We get 
Set A contains the positive even integers less than 14. Set B contains the positive multiples of three less than 20. What is the intersection of the two sets?
A∩B = { }
A∩B = {6, 12}
A∩B = {4, 6, 8}
A∩B = {6}
A∩B = {6, 12, 18}
Explanation
A = {2, 4, 6, 8, 10, 12}
B = {3, 6, 9, 12, 15, 18}
The intersection of a set means that the elements are in both sets: A∩B = {6, 12}
Set A contains the positive even integers less than 14. Set B contains the positive multiples of three less than 20. What is the intersection of the two sets?
A∩B = { }
A∩B = {6, 12}
A∩B = {4, 6, 8}
A∩B = {6}
A∩B = {6, 12, 18}
Explanation
A = {2, 4, 6, 8, 10, 12}
B = {3, 6, 9, 12, 15, 18}
The intersection of a set means that the elements are in both sets: A∩B = {6, 12}
We have two sports clubs offered to a class of 100 students. 70 students joined the basketball club, 40 students joined the swimming club, and 10 students joined neither. How many students joined both the swimming club and the basketball club?
Explanation
The idea is to draw a Venn Diagram and find the intersection. We have one circle of 70 and another with 40. When we add the two circles plus the 10 students who joined neither, we should get 100 students. However, when adding the two circles, we are adding the intersections twice, therefore we need to subtract the intersection once.
We get 
The universal set is positive counting numbers less than 11. Set A = {1, 3, 5} and Set B = { 2, 4, 6}.
What is 
Explanation


U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 3, 5}
A' = {2, 4, 6, 7, 8, 9, 10}
B = {2, 4, 6}
B' = {1, 3, 5, 7, 8, 9, 10}



In a class of senior high-school students, 



Explanation
A Venn diagram can help us determine the total number of students in the class.
First, we must calculate the number of students who have ONLY cats or ONLY dogs. First, for cats, 15 students have cats, and 5 students have both cats and dogs.
Ten students have only cats.
For dogs, 12 students have dogs, and 5 students have both cats and dogs.
Seven students have only dogs.
Using this information, we can fill in the Venn diagram.

This diagram shows the 10 students with only cats, the 7 students with only dogs, the 5 students with both, and the 8 students with neither. Adding up the numbers will give us the total number of students.