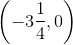PSAT Math - How to find x or y intercept

Determine the y-intercept of the following line:

$\dpi{100} \small 3x+6y=9$

$\dpi{100} \small 1.5$

$\dpi{100} \small 3$

$\dpi{100} \small 6$

$\dpi{100} \small 9$

$\dpi{100} \small \frac{1}{3}$

Explanation

The y-intercept occurs when $\dpi{100} \small x=0$

$\dpi{100} \small 3x+6y=9$

$\dpi{100} \small 3(0)+6y=9$

$\dpi{100} \small 0+6y=9$

$\dpi{100} \small y = \frac{9}{6}=1.5$

Find the x-intercepts of $25x^{2}+4y^{2} = 9$ .

$\pm \frac{3}{5}$

$\frac{3}{5}$

$5$

$2$

$\pm 5$

Explanation

To find the x-intercepts, plug $y=0$ into the equation and solve for $x$ .

$25x^{2} + 4\cdot 0^{2} = 9$

$25x^{2} = 9$

$x^{2} = \frac{9}{25}$

$x = \pm \frac{3}{5}$

Don't forget that there are two solutions, both negative and positive!

Where does the line given by $y=3(x-4)-9$ intercept the -axis?

$\frac{4}{3}$

Explanation

First, put in slope-intercept form.

$y=3x-21$ .

To find the -intercept, set and solve for .

Which of the following lines does not intersect the line ?

$y=\frac{1}{4}x-7$

$y=-\frac{1}{4}x+11$

Explanation

Parallel lines never intersect, so you are looking for a line that has the same slope as the one given. The slope of the given line is –4, and the slope of the line in y = –4_x_ + 5 is –4 as well. Since these two lines have equal slopes, they will run parallel and can never intersect.

If these three points are on a single line, what is the formula for the line?

(3,3)

(4,7)

(5,11)

y = 4x - 9

y = 4x + 31

y = 3x - 3

y = 3x - 9

y = 5x + 11

Explanation

Formula for a line: y = mx + b

First find slope from two of the points: (3,3) and (4,7)

m = slope = (y2 – y1) / x2 – x1) = (7-3) / (4-3) = 4 / 1 = 4

Solve for b by plugging m and one set of coordinates into the formula for a line:

y = mx + b

11 = 4 * 5 + b

11 = 20 + b

b = -9

y = 4x - 9

What is the y intercept of the following function of x?

y = 3x

–3

–1

Explanation

The answer is 0 because in slope intercept form, y = mx + b; b is the y intercept. In this case b = 0.

Given the line , what is the sum of the -intercept and the -intercept?

Explanation

Intercepts occur when a line crosses the -axis or the -axis. When the line crosses the -axis, then and . When the line crosses the -axis, then and . The intercept points are and . So the -intercept is and the intercept is and the sum is .