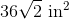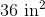How to find the surface area of a tetrahedron

Help Questions

PSAT Math › How to find the surface area of a tetrahedron

Questions 1 - 2

A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.

A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.

$36 \sqrt{3}\textrm{ in}^{2}$

$9 \sqrt{3}\textrm{ in}^{2}$

$36 \sqrt{2}\textrm{ in}^{2}$

$9 \sqrt{2}\textrm{ in}^{2}$

$36 \textrm{ in}^{2}$

The area of an equilateral triangle is given by the formula

$A = \frac{s^{2}\sqrt{3}}{4}$

Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is

$SA = 4 A = 4 \cdot \frac{s^{2}\sqrt{3}}{4} = s^{2}\sqrt{3}$

Substitute :

$SA = s^{2}\sqrt{3} = 6^{2}\sqrt{3} = 36\sqrt{3}$ square inches.

Tetra_1

Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.

Insufficient information is given to answer the question.

The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area

$A = \frac{s^{2} \sqrt{3} }{4} = \frac{7^{2} \sqrt{3} }{4} = \frac{49 \sqrt{3} }{4} \approx \frac{49 \cdot 1.7321}{4} \approx 21.22$

The total surface area is four times this, or about $4 \cdot 21.22 = 84.88$ .

Rounded, this is 84.9.