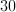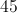How to find an angle in an acute / obtuse isosceles triangle
Help Questions
PSAT Math › How to find an angle in an acute / obtuse isosceles triangle
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
Explanation
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
Thus the vertex angle is 34 and the base angles are 73.
Triangle ABC has angle measures as follows:
What is 
57
19
79
44
90
Explanation
The sum of the measures of the angles of a triangle is 180.
Thus we set up the equation
After combining like terms and cancelling, we have
Thus
In an isosceles triangle, the vertex angle is 15 less than the base angle. What is the base angle?
Explanation
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
Thus, 65 is the base angle and 50 is the vertex angle.
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is 
Explanation
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:
Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
The base angle of an isosceles triangle is 
Explanation
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation 
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is 
The base angle of an isosceles triangle is 10 more than twice the vertex angle. What is the vertex angle?
Explanation
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
The vertex angle is 32 degrees and the base angle is 74 degrees
The base angle of an isosceles triangle is ten less than twice the vertex angle. What is the vertex angle?
Explanation
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
So the vertex angle is 40 and the base angles is 70
In an isosceles triangle the vertex angle is half the base angle. What is the vertex angle?
Explanation
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes