Polynomial Operations
Help Questions
PSAT Math › Polynomial Operations
Explanation
Step 1: Distribute the negative to the second polynomial:
Step 2: Combine like terms:
Explanation
Step 1: Distribute the negative to the second polynomial:
Step 2: Combine like terms:
Add the polynomials.
Explanation
We can add together each of the terms of the polynomial which have the same degree for our variable.
Add the polynomials.
Explanation
We can add together each of the terms of the polynomial which have the same degree for our variable.
Which of these polynomials has the greatest degree?
All of the polynomials given in the other responses have the same degree.
Explanation
The degree of a polynomial is the highest degree of any term; the degree of a term is the exponent of its variable or the sum of the exponents of its variables, with unwritten exponents being equal to 1. For each term in a polynomial, write the exponent or add the exponents; the greatest number is its degree. We do this with all four choices:


The degree of this polynomial is 5.
The degree of this polynomial is 5.
The degree of this polynomial is 5.
The degree of this polynomial is 5.
All four polynomials have the same degree.
Which of these polynomials has the greatest degree?
All of the polynomials given in the other responses have the same degree.
Explanation
The degree of a polynomial is the highest degree of any term; the degree of a term is the exponent of its variable or the sum of the exponents of its variables, with unwritten exponents being equal to 1. For each term in a polynomial, write the exponent or add the exponents; the greatest number is its degree. We do this with all four choices:


The degree of this polynomial is 5.
The degree of this polynomial is 5.
The degree of this polynomial is 5.
The degree of this polynomial is 5.
All four polynomials have the same degree.
Multiply:
Explanation
This product fits the sum of cubes pattern, where 
So
Give the degree of the polynomial
Explanation
The degree of a polynomial in one variable is the greatest exponent of any of the powers of the variable. The terms have as their exponents, in order, 44, 20, 10, and 100; the greatest of these is 100, which is the degree.
Multiply:
Explanation
This product fits the sum of cubes pattern, where 
So
Give the degree of the polynomial
Explanation
The degree of a polynomial in one variable is the greatest exponent of any of the powers of the variable. The terms have as their exponents, in order, 44, 20, 10, and 100; the greatest of these is 100, which is the degree.











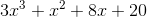


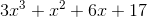


























](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/210807/gif.latex)

](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/210810/gif.latex)






