Acute / Obtuse Triangles - PSAT Math
Card 0 of 175
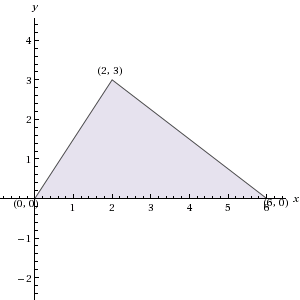
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Compare your answer with the correct one above
The height, 
, of triangle 
in the figure is one-fourth the length of 
. In terms of h, what is the area of triangle 
?
The height, 
If 
*
, then the length of 
must be 
.
Using the formula for the area of a triangle (
), with 
, the area of the triangle must be 
.
If
Using the formula for the area of a triangle (
Compare your answer with the correct one above
You are given triangles 
and 
, with 
and 
. Which of these statements, along with what you are given, is not enough to prove that 
?
I) 
and 
have the same perimeter
II) 
III) 
You are given triangles
I)
II)
III)
If 
and 
have the same perimeter, 
, and 
, it follows that 
. The three triangles have the same sidelengths, setting the conditions for the Side-Side-Side Congruence Postulate.
If 
, then, since the sum of the degree measures of both triangles is the same (180 degrees), it follows that 
. Since 
and 
are congruent included angles of congruent sides, this sets the conditions for the SAS Congruence Postulate.
In both of the above cases, it follows that 
.
However, similarly to the previous situation, if 
, then it follows that 
, meaning that we have congruent sides and congruent nonincluded angles. However, this is not sufficient to prove congruence.
"Statement III" is the correct response.
If
If
In both of the above cases, it follows that
However, similarly to the previous situation, if
"Statement III" is the correct response.
Compare your answer with the correct one above
If a = 7 and b = 4, which of the following could be the perimeter of the triangle?
I. 11
II. 15
III. 25
If a = 7 and b = 4, which of the following could be the perimeter of the triangle?
I. 11
II. 15
III. 25
Consider the perimeter of a triangle:
P = a + b + c
Since we know a and b, we can find c.
In I:
11 = 7 + 4 + c
11 = 11 + c
c = 0
Note that if c = 0, the shape is no longer a trial. Thus, we can eliminate I.
In II:
15 = 7 + 4 + c
15 = 11 + c
c = 4.
This is plausible given that the other sides are 7 and 4.
In III:
25 = 7 + 4 + c
25 = 11 + c
c = 14.
It is not possible for one side of a triangle to be greater than the sum of both of the other sides, so eliminate III.
Thus we are left with only II.
Consider the perimeter of a triangle:
P = a + b + c
Since we know a and b, we can find c.
In I:
11 = 7 + 4 + c
11 = 11 + c
c = 0
Note that if c = 0, the shape is no longer a trial. Thus, we can eliminate I.
In II:
15 = 7 + 4 + c
15 = 11 + c
c = 4.
This is plausible given that the other sides are 7 and 4.
In III:
25 = 7 + 4 + c
25 = 11 + c
c = 14.
It is not possible for one side of a triangle to be greater than the sum of both of the other sides, so eliminate III.
Thus we are left with only II.
Compare your answer with the correct one above
Find the height of a triangle if the area of the triangle = 18 and the base = 4.
Find the height of a triangle if the area of the triangle = 18 and the base = 4.
The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.
The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.
Compare your answer with the correct one above
and 
are similar triangles. The perimeter of Triangle A is 45” and the length of two of its sides are 15” and 10”. If the perimeter of Triangle B is 135” and what are lengths of two of its sides?
The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is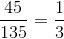 
.
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“
The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is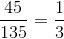
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“
Compare your answer with the correct one above
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
Compare your answer with the correct one above
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
Compare your answer with the correct one above
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
Compare your answer with the correct one above
The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?
The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?
Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:
x + 7 > 9
x + 9 > 7
7 + 9 > x
We can solve these three inequalities to determine the possible values of x.
x + 7 > 9
Subtract 7 from both sides.
x > 2
Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain
x > –2
Finally, 7 + 9 > x, which means that 16 > x.
Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.
The answer is 12.
Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:
x + 7 > 9
x + 9 > 7
7 + 9 > x
We can solve these three inequalities to determine the possible values of x.
x + 7 > 9
Subtract 7 from both sides.
x > 2
Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain
x > –2
Finally, 7 + 9 > x, which means that 16 > x.
Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.
The answer is 12.
Compare your answer with the correct one above
A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?
A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?
The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.
The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.
Compare your answer with the correct one above
Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.
Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.
Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.
Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.
Compare your answer with the correct one above
The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?
The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?
According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:
x + 8 > 12
x + 12 > 8
8 + 12 > x
Let's solve each inequality.
x + 8 > 12
Subtract 8 from both sides.
x > 4
Next, let's look at the inequality x + 12 > 8
x + 12 > 8
Subtract 12 from both sides.
x > –4
Lastly, 8 + 12 > x, which means that x < 20.
This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.
To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.
The answer is 4 < x < 20.
According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:
x + 8 > 12
x + 12 > 8
8 + 12 > x
Let's solve each inequality.
x + 8 > 12
Subtract 8 from both sides.
x > 4
Next, let's look at the inequality x + 12 > 8
x + 12 > 8
Subtract 12 from both sides.
x > –4
Lastly, 8 + 12 > x, which means that x < 20.
This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.
To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.
The answer is 4 < x < 20.
Compare your answer with the correct one above
If 2 sides of the triangle are have lengths equal to 8 and 14, what is one possible length of the third side?
If 2 sides of the triangle are have lengths equal to 8 and 14, what is one possible length of the third side?
The sum of the lengths of 2 sides of a triangle must be greater than—but not equal to—the length of the third side. Further, the third side must be longer than the difference between the greater and the lesser of the other two sides; therefore, 20 is the only possible answer.
The sum of the lengths of 2 sides of a triangle must be greater than—but not equal to—the length of the third side. Further, the third side must be longer than the difference between the greater and the lesser of the other two sides; therefore, 20 is the only possible answer.
Compare your answer with the correct one above
In 
the length of AB is 15 and the length of side AC is 5. What is the least possible integer length of side BC?
In
Rule - the length of one side of a triangle must be greater than the differnce and less than the sum of the lengths of the other two sides.
Given lengths of two of the sides of the 
are 15 and 5. The length of the third side must be greater than 15-5 or 10 and less than 15+5 or 20.
The question asks what is the least possible integer length of BC, which would be 11
Rule - the length of one side of a triangle must be greater than the differnce and less than the sum of the lengths of the other two sides.
Given lengths of two of the sides of the
The question asks what is the least possible integer length of BC, which would be 11
Compare your answer with the correct one above
All of the following could be the possible side lengths of a triangle EXCEPT:
All of the following could be the possible side lengths of a triangle EXCEPT:
The length of the third side of a triangle must always be between (but not equal to) the sum and the difference of the other two sides.
For instance, take the example of 2, 6, and 7.
and 
. Therefore, the third side length must be greater than 4 and less than 8. Because 7 is greater than 4 and less than 8, it is possible for these to be the side lengths of a triangle.
The 5, 7, 12 answer choice is the only option for which this is not the case.
and 
. Therefore, the third side length must be between 2 and 12. Because it is equal to the sum, not less than the sum, it is not possible that these could be the side lengths of a triangle.
The length of the third side of a triangle must always be between (but not equal to) the sum and the difference of the other two sides.
For instance, take the example of 2, 6, and 7.
The 5, 7, 12 answer choice is the only option for which this is not the case.
Compare your answer with the correct one above
Which of the following describes a triangle with sides of length 14 inches, 18 inches, and 2 feet?
Which of the following describes a triangle with sides of length 14 inches, 18 inches, and 2 feet?
2 feet is equal to 24 inches,so the sides of the triangle measure 14, 18, and 24.
First, we test to make sure the triangle exists. By the Triangle Inequality, for this to exist, the sum of the two smaller sidelengths must exceed the third, which we can see is the case:
The three sidelengths are all unequal, so the triangle is scalene.
Finally, we compare the sum of the squares of the smaller sidelengths to the square of the third:
Since
,
the triangle is obtuse.
The correct response is that the triangle is scalene and obtuse.
2 feet is equal to 24 inches,so the sides of the triangle measure 14, 18, and 24.
First, we test to make sure the triangle exists. By the Triangle Inequality, for this to exist, the sum of the two smaller sidelengths must exceed the third, which we can see is the case:
The three sidelengths are all unequal, so the triangle is scalene.
Finally, we compare the sum of the squares of the smaller sidelengths to the square of the third:
Since
the triangle is obtuse.
The correct response is that the triangle is scalene and obtuse.
Compare your answer with the correct one above
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
Compare your answer with the correct one above
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
Compare your answer with the correct one above
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
Compare your answer with the correct one above