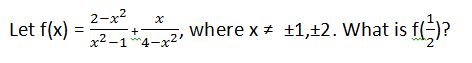Rational Expressions - PSAT Math
Card 1 of 70
If √(ab) = 8, and _a_2 = b, what is a?
If √(ab) = 8, and _a_2 = b, what is a?
Tap to reveal answer
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
Tap to reveal answer
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
← Didn't Know|Knew It →
what is 6/8 X 20/3
what is 6/8 X 20/3
Tap to reveal answer
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
← Didn't Know|Knew It →
Which of the following is equivalent to $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} ? Assume that denominators are always nonzero.
Which of the following is equivalent to $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} ? Assume that denominators are always nonzero.
Tap to reveal answer
We will need to simplify the expression $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We can think of this as a large fraction with a numerator of $\frac{1}{t}$-$\frac{1}{x}$ and a denominator of x-t.
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\frac{1}{t}$ has a denominator of t, and -$\frac{1}{x}$ has a denominator of x. The least common denominator that these two fractions have in common is xt. Thus, we are going to write equivalent fractions with denominators of xt.
In order to convert the fraction $\frac{1}{t}$ to a denominator with xt, we will need to multiply the top and bottom by x.
$\frac{1}{t}$=\frac{1cdot x}{tcdot x}$=\frac{x}{xt}$
Similarly, we will multiply the top and bottom of -$\frac{1}{x}$ by t.
$\frac{1}{x}$=\frac{1cdot t}{xcdot t}$=\frac{t}{xt}$
We can now rewrite $\frac{1}{t}$-$\frac{1}{x}$ as follows:
$\frac{1}{t}$-$\frac{1}{x}$ = $\frac{x}{xt}$-$\frac{t}{xt}$=\frac{x-t}{xt}$
Let's go back to the original fraction $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We will now rewrite the numerator:
$\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} = $\frac{frac{x-t}{xt}$}{x-t}
To simplify this further, we can think of $\frac{frac{x-t}{xt}$}{x-t} as the same as $\frac{x-t}{xt}$div (x-t) . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, adiv b=acdot $\frac{1}{b}$.
$\frac{x-t}{xt}$div (x-t) = $\frac{x-t}{xt}$cdot $\frac{1}{x-t}$=\frac{x-t}{xt(x-t)}$= $\frac{1}{xt}$
Lastly, we will use the property of exponents which states that, in general, $$\frac{1}{a}$=a^{-1}$.
$$\frac{1}{xt}$=(xt)^{-1}$
The answer is $(xt)^{-1}$.
We will need to simplify the expression $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We can think of this as a large fraction with a numerator of $\frac{1}{t}$-$\frac{1}{x}$ and a denominator of x-t.
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\frac{1}{t}$ has a denominator of t, and -$\frac{1}{x}$ has a denominator of x. The least common denominator that these two fractions have in common is xt. Thus, we are going to write equivalent fractions with denominators of xt.
In order to convert the fraction $\frac{1}{t}$ to a denominator with xt, we will need to multiply the top and bottom by x.
$\frac{1}{t}$=\frac{1cdot x}{tcdot x}$=\frac{x}{xt}$
Similarly, we will multiply the top and bottom of -$\frac{1}{x}$ by t.
$\frac{1}{x}$=\frac{1cdot t}{xcdot t}$=\frac{t}{xt}$
We can now rewrite $\frac{1}{t}$-$\frac{1}{x}$ as follows:
$\frac{1}{t}$-$\frac{1}{x}$ = $\frac{x}{xt}$-$\frac{t}{xt}$=\frac{x-t}{xt}$
Let's go back to the original fraction $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We will now rewrite the numerator:
$\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} = $\frac{frac{x-t}{xt}$}{x-t}
To simplify this further, we can think of $\frac{frac{x-t}{xt}$}{x-t} as the same as $\frac{x-t}{xt}$div (x-t) . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, adiv b=acdot $\frac{1}{b}$.
$\frac{x-t}{xt}$div (x-t) = $\frac{x-t}{xt}$cdot $\frac{1}{x-t}$=\frac{x-t}{xt(x-t)}$= $\frac{1}{xt}$
Lastly, we will use the property of exponents which states that, in general, $$\frac{1}{a}$=a^{-1}$.
$$\frac{1}{xt}$=(xt)^{-1}$
The answer is $(xt)^{-1}$.
← Didn't Know|Knew It →
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Tap to reveal answer
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
← Didn't Know|Knew It →
Simplify.

Simplify.
Tap to reveal answer

Same denominator means you add straight across the numerators, keeping the denominator the same.

Add like terms.

Final Answer.

Same denominator means you add straight across the numerators, keeping the denominator the same.
Add like terms.
Final Answer.
← Didn't Know|Knew It →
Simplify.

Simplify.
Tap to reveal answer

Check for same Denominator

Add like terms

Check for GCF or if the expression can be factored

After factoring, divide out like terms. 

Final Answer
Check for same Denominator
Add like terms
Check for GCF or if the expression can be factored
After factoring, divide out like terms.
Final Answer
← Didn't Know|Knew It →
Which of the following is equivalent to $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} ? Assume that denominators are always nonzero.
Which of the following is equivalent to $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} ? Assume that denominators are always nonzero.
Tap to reveal answer
We will need to simplify the expression $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We can think of this as a large fraction with a numerator of $\frac{1}{t}$-$\frac{1}{x}$ and a denominator of x-t.
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\frac{1}{t}$ has a denominator of t, and -$\frac{1}{x}$ has a denominator of x. The least common denominator that these two fractions have in common is xt. Thus, we are going to write equivalent fractions with denominators of xt.
In order to convert the fraction $\frac{1}{t}$ to a denominator with xt, we will need to multiply the top and bottom by x.
$\frac{1}{t}$=\frac{1cdot x}{tcdot x}$=\frac{x}{xt}$
Similarly, we will multiply the top and bottom of -$\frac{1}{x}$ by t.
$\frac{1}{x}$=\frac{1cdot t}{xcdot t}$=\frac{t}{xt}$
We can now rewrite $\frac{1}{t}$-$\frac{1}{x}$ as follows:
$\frac{1}{t}$-$\frac{1}{x}$ = $\frac{x}{xt}$-$\frac{t}{xt}$=\frac{x-t}{xt}$
Let's go back to the original fraction $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We will now rewrite the numerator:
$\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} = $\frac{frac{x-t}{xt}$}{x-t}
To simplify this further, we can think of $\frac{frac{x-t}{xt}$}{x-t} as the same as $\frac{x-t}{xt}$div (x-t) . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, adiv b=acdot $\frac{1}{b}$.
$\frac{x-t}{xt}$div (x-t) = $\frac{x-t}{xt}$cdot $\frac{1}{x-t}$=\frac{x-t}{xt(x-t)}$= $\frac{1}{xt}$
Lastly, we will use the property of exponents which states that, in general, $$\frac{1}{a}$=a^{-1}$.
$$\frac{1}{xt}$=(xt)^{-1}$
The answer is $(xt)^{-1}$.
We will need to simplify the expression $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We can think of this as a large fraction with a numerator of $\frac{1}{t}$-$\frac{1}{x}$ and a denominator of x-t.
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\frac{1}{t}$ has a denominator of t, and -$\frac{1}{x}$ has a denominator of x. The least common denominator that these two fractions have in common is xt. Thus, we are going to write equivalent fractions with denominators of xt.
In order to convert the fraction $\frac{1}{t}$ to a denominator with xt, we will need to multiply the top and bottom by x.
$\frac{1}{t}$=\frac{1cdot x}{tcdot x}$=\frac{x}{xt}$
Similarly, we will multiply the top and bottom of -$\frac{1}{x}$ by t.
$\frac{1}{x}$=\frac{1cdot t}{xcdot t}$=\frac{t}{xt}$
We can now rewrite $\frac{1}{t}$-$\frac{1}{x}$ as follows:
$\frac{1}{t}$-$\frac{1}{x}$ = $\frac{x}{xt}$-$\frac{t}{xt}$=\frac{x-t}{xt}$
Let's go back to the original fraction $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We will now rewrite the numerator:
$\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} = $\frac{frac{x-t}{xt}$}{x-t}
To simplify this further, we can think of $\frac{frac{x-t}{xt}$}{x-t} as the same as $\frac{x-t}{xt}$div (x-t) . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, adiv b=acdot $\frac{1}{b}$.
$\frac{x-t}{xt}$div (x-t) = $\frac{x-t}{xt}$cdot $\frac{1}{x-t}$=\frac{x-t}{xt(x-t)}$= $\frac{1}{xt}$
Lastly, we will use the property of exponents which states that, in general, $$\frac{1}{a}$=a^{-1}$.
$$\frac{1}{xt}$=(xt)^{-1}$
The answer is $(xt)^{-1}$.
← Didn't Know|Knew It →
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Tap to reveal answer
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
← Didn't Know|Knew It →
Simplify.

Simplify.
Tap to reveal answer

Same denominator means you add straight across the numerators, keeping the denominator the same.

Add like terms.

Final Answer.

Same denominator means you add straight across the numerators, keeping the denominator the same.
Add like terms.
Final Answer.
← Didn't Know|Knew It →
Simplify.

Simplify.
Tap to reveal answer

Check for same Denominator

Add like terms

Check for GCF or if the expression can be factored

After factoring, divide out like terms. 

Final Answer
Check for same Denominator
Add like terms
Check for GCF or if the expression can be factored
After factoring, divide out like terms.
Final Answer
← Didn't Know|Knew It →
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
Tap to reveal answer
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
← Didn't Know|Knew It →
what is 6/8 X 20/3
what is 6/8 X 20/3
Tap to reveal answer
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
← Didn't Know|Knew It →
Simplify.
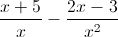
Simplify.
Tap to reveal answer

Determine an LCD (Least Common Denominator) between 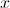 and
and 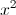 .
.
LCD = 
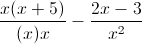
Multiply the top and bottom of the first rational expression by  , so that the denominator will be
, so that the denominator will be  .
.
Distribute the  to
to  .
.

Now you can subtract because both rational expressions have the same denominators.

Final Answer.
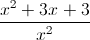
Determine an LCD (Least Common Denominator) between 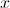
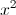
LCD =
Multiply the top and bottom of the first rational expression by 

Distribute the 

Now you can subtract because both rational expressions have the same denominators.
Final Answer.
← Didn't Know|Knew It →
Simplify.
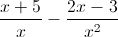
Simplify.
Tap to reveal answer

Determine an LCD (Least Common Denominator) between 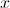 and
and 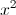 .
.
LCD = 
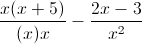
Multiply the top and bottom of the first rational expression by  , so that the denominator will be
, so that the denominator will be  .
.
Distribute the  to
to  .
.

Now you can subtract because both rational expressions have the same denominators.

Final Answer.
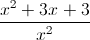
Determine an LCD (Least Common Denominator) between 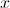
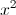
LCD =
Multiply the top and bottom of the first rational expression by 

Distribute the 

Now you can subtract because both rational expressions have the same denominators.
Final Answer.
← Didn't Know|Knew It →
If √(ab) = 8, and _a_2 = b, what is a?
If √(ab) = 8, and _a_2 = b, what is a?
Tap to reveal answer
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
Tap to reveal answer
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
← Didn't Know|Knew It →
what is 6/8 X 20/3
what is 6/8 X 20/3
Tap to reveal answer
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
← Didn't Know|Knew It →