How to find the area of an acute / obtuse triangle - PSAT Math
Card 0 of 14
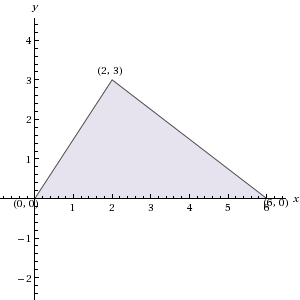
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Compare your answer with the correct one above
The height, 
, of triangle 
in the figure is one-fourth the length of 
. In terms of h, what is the area of triangle 
?
The height, 
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
Compare your answer with the correct one above
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Compare your answer with the correct one above
The height, , of triangle in the figure is one-fourth the length of . In terms of h, what is the area of triangle ?
The height,
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
Compare your answer with the correct one above
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Compare your answer with the correct one above
The height, , of triangle in the figure is one-fourth the length of . In terms of h, what is the area of triangle ?
The height,
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
Compare your answer with the correct one above
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Compare your answer with the correct one above
The height, , of triangle in the figure is one-fourth the length of . In terms of h, what is the area of triangle ?
The height,
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
Compare your answer with the correct one above
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Compare your answer with the correct one above
The height, , of triangle in the figure is one-fourth the length of . In terms of h, what is the area of triangle ?
The height,
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
Compare your answer with the correct one above
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Compare your answer with the correct one above
The height, , of triangle in the figure is one-fourth the length of . In terms of h, what is the area of triangle ?
The height,
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
Compare your answer with the correct one above
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.
Compare your answer with the correct one above
The height, , of triangle in the figure is one-fourth the length of . In terms of h, what is the area of triangle ?
The height,
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.
Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.
Compare your answer with the correct one above