Solid Geometry - PSAT Math
Card 1 of 1015
A spherical orange fits snugly inside a small cubical box such that each of the six walls of the box just barely touches the surface of the orange. If the volume of the box is 64 cubic inches, what is the surface area of the orange in square inches?
A spherical orange fits snugly inside a small cubical box such that each of the six walls of the box just barely touches the surface of the orange. If the volume of the box is 64 cubic inches, what is the surface area of the orange in square inches?
Tap to reveal answer
The volume of a cube is found by V = s3. Since V = 64, s = 4. The side of the cube is the same as the diameter of the sphere. Since d = 4, r = 2. The surface area of a sphere is found by SA = 4π(r2) = 4π(22) = 16π.
The volume of a cube is found by V = s3. Since V = 64, s = 4. The side of the cube is the same as the diameter of the sphere. Since d = 4, r = 2. The surface area of a sphere is found by SA = 4π(r2) = 4π(22) = 16π.
← Didn't Know|Knew It →
A solid sphere is cut in half to form two solid hemispheres. What is the ratio of the surface area of one of the hemispheres to the surface area of the entire sphere before it was cut?
A solid sphere is cut in half to form two solid hemispheres. What is the ratio of the surface area of one of the hemispheres to the surface area of the entire sphere before it was cut?
Tap to reveal answer
The surface area of the sphere before it was cut is equal to the following:
surface area of solid sphere = 4_πr_2, where r is the length of the radius.
Each hemisphere will have the following shape:
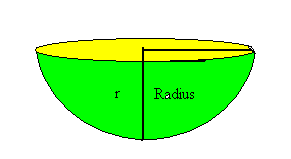
In order to determine the surface area of the hemisphere, we must find the surface area of the flat region and the curved region. The flat region will have a surface area equal to the area of a circle with radius r.
area of flat part of hemisphere = _πr_2
The surface area of the curved portion of the hemisphere will equal one-half of the surface area of the uncut sphere, which we established to be 4_πr_2.
area of curved part of hemisphere = (1/2)4_πr_2 = 2_πr_2
The total surface area of the hemisphere will be equal to the sum of the surface areas of the flat part and curved part of the hemisphere.
total surface area of hemisphere = _πr_2 + 2_πr_2 = 3_πr_2
Finally, we must find the ratio of the surface area of the hemisphere to the surface area of the uncut sphere.
ratio = (3_πr_2)/(4_πr_2) = 3/4
The answer is 3/4.
The surface area of the sphere before it was cut is equal to the following:
surface area of solid sphere = 4_πr_2, where r is the length of the radius.
Each hemisphere will have the following shape:
In order to determine the surface area of the hemisphere, we must find the surface area of the flat region and the curved region. The flat region will have a surface area equal to the area of a circle with radius r.
area of flat part of hemisphere = _πr_2
The surface area of the curved portion of the hemisphere will equal one-half of the surface area of the uncut sphere, which we established to be 4_πr_2.
area of curved part of hemisphere = (1/2)4_πr_2 = 2_πr_2
The total surface area of the hemisphere will be equal to the sum of the surface areas of the flat part and curved part of the hemisphere.
total surface area of hemisphere = _πr_2 + 2_πr_2 = 3_πr_2
Finally, we must find the ratio of the surface area of the hemisphere to the surface area of the uncut sphere.
ratio = (3_πr_2)/(4_πr_2) = 3/4
The answer is 3/4.
← Didn't Know|Knew It →
The volume of a sphere is 2304_π_ in3. What is the surface area of this sphere in square inches?
The volume of a sphere is 2304_π_ in3. What is the surface area of this sphere in square inches?
Tap to reveal answer
To solve this, we must first begin by finding the radius of the sphere. To do this, recall that the volume of a sphere is:
V = (4/3)_πr_3
For our data, we can say:
2304_π_ = (4/3)_πr_3; 2304 = (4/3)_r_3; 6912 = 4_r_3; 1728 = _r_3; 12 * 12 * 12 = _r_3; r = 12
Now, based on this, we can ascertain the surface area using the equation:
A = 4_πr_2
For our data, this is:
A = 4_π_*122 = 576_π_
To solve this, we must first begin by finding the radius of the sphere. To do this, recall that the volume of a sphere is:
V = (4/3)_πr_3
For our data, we can say:
2304_π_ = (4/3)_πr_3; 2304 = (4/3)_r_3; 6912 = 4_r_3; 1728 = _r_3; 12 * 12 * 12 = _r_3; r = 12
Now, based on this, we can ascertain the surface area using the equation:
A = 4_πr_2
For our data, this is:
A = 4_π_*122 = 576_π_
← Didn't Know|Knew It →
A sphere has its center at the origin. A point on its surface is found on the x-y axis at (6,8). In square units, what is the surface area of this sphere?
A sphere has its center at the origin. A point on its surface is found on the x-y axis at (6,8). In square units, what is the surface area of this sphere?
Tap to reveal answer
To find the surface area, we must first find the radius. Based on our description, this passes from (0,0) to (6,8). This can be found using the distance formula:
62 + 82 = _r_2; _r_2 = 36 + 64; _r_2 = 100; r = 10
It should be noted that you could have quickly figured this out by seeing that (6,8) is the hypotenuse of a 6-8-10 triangle (which is a multiple of the "easy" 3-4-5).
The rest is easy. The surface area of the sphere is defined by:
A = 4_πr_2 = 4 * 100 * π = 400_π_
To find the surface area, we must first find the radius. Based on our description, this passes from (0,0) to (6,8). This can be found using the distance formula:
62 + 82 = _r_2; _r_2 = 36 + 64; _r_2 = 100; r = 10
It should be noted that you could have quickly figured this out by seeing that (6,8) is the hypotenuse of a 6-8-10 triangle (which is a multiple of the "easy" 3-4-5).
The rest is easy. The surface area of the sphere is defined by:
A = 4_πr_2 = 4 * 100 * π = 400_π_
← Didn't Know|Knew It →
A sphere is perfectly contained within a cube that has a surface area of 726 square units. In square units, what is the surface area of the sphere?
A sphere is perfectly contained within a cube that has a surface area of 726 square units. In square units, what is the surface area of the sphere?
Tap to reveal answer
To begin, we must determine the dimensions of the cube. To do this, recall that the surface area of a cube is made up of six squares and is thus defined as: A = 6_s_2, where s is one of the sides of the cube. For our data, this gives us:
726 = 6_s_2; 121 = _s_2; s = 11
Now, if the sphere is contained within the cube, that means that 11 represents the diameter of the sphere. Therefore, the radius of the sphere is 5.5 units. The surface area of a sphere is defined as: A = 4_πr_2. For our data, that would be:
A = 4_π_ * 5.52 = 30.25 * 4 * π = 121_π_
To begin, we must determine the dimensions of the cube. To do this, recall that the surface area of a cube is made up of six squares and is thus defined as: A = 6_s_2, where s is one of the sides of the cube. For our data, this gives us:
726 = 6_s_2; 121 = _s_2; s = 11
Now, if the sphere is contained within the cube, that means that 11 represents the diameter of the sphere. Therefore, the radius of the sphere is 5.5 units. The surface area of a sphere is defined as: A = 4_πr_2. For our data, that would be:
A = 4_π_ * 5.52 = 30.25 * 4 * π = 121_π_
← Didn't Know|Knew It →
The area of a circle with radius 4 divided by the surface area of a sphere with radius 2 is equal to:
The area of a circle with radius 4 divided by the surface area of a sphere with radius 2 is equal to:
Tap to reveal answer
The surface area of a sphere is 4_πr_2. The area of a circle is _πr_2. 16/16 is equal to 1.
The surface area of a sphere is 4_πr_2. The area of a circle is _πr_2. 16/16 is equal to 1.
← Didn't Know|Knew It →
What is the ratio of the surface area of a cube to the surface area of a sphere inscribed within it?
What is the ratio of the surface area of a cube to the surface area of a sphere inscribed within it?
Tap to reveal answer
Let's call the radius of the sphere r. The formula for the surface area of a sphere (A) is given below:
A = 4_πr_2
Because the sphere is inscribed inside the cube, the diameter of the sphere is equal to the side length of the cube. Because the diameter is twice the length of the radius, the diameter of the sphere is 2_r_. This means that the side length of the cube is also 2_r_.
The surface area for a cube is given by the following formula, where s represents the length of each side of the cube:
surface area of cube = 6_s_2
The formula for surface area of a cube comes from the fact that each face of the cube has an area of _s_2, and there are 6 faces total on a cube.
Since we already determined that the side length of the cube is the same as 2_r_, we can replace s with 2_r_.
surface area of cube = 6(2_r_)2 = 6(2_r_)(2_r_) = 24_r_2.
We are asked to find the ratio of the surface area of the cube to the surface area of the sphere. This means we must divide the surface area of the cube by the surface area of the sphere.
ratio = (24_r_2)/(4_πr_2)
The _r_2 term cancels in the numerator and denominator. Also, 24/4 simplifes to 6.
ratio = (24_r_2)/(4_πr_2) = 6/π
The answer is 6/π.
Let's call the radius of the sphere r. The formula for the surface area of a sphere (A) is given below:
A = 4_πr_2
Because the sphere is inscribed inside the cube, the diameter of the sphere is equal to the side length of the cube. Because the diameter is twice the length of the radius, the diameter of the sphere is 2_r_. This means that the side length of the cube is also 2_r_.
The surface area for a cube is given by the following formula, where s represents the length of each side of the cube:
surface area of cube = 6_s_2
The formula for surface area of a cube comes from the fact that each face of the cube has an area of _s_2, and there are 6 faces total on a cube.
Since we already determined that the side length of the cube is the same as 2_r_, we can replace s with 2_r_.
surface area of cube = 6(2_r_)2 = 6(2_r_)(2_r_) = 24_r_2.
We are asked to find the ratio of the surface area of the cube to the surface area of the sphere. This means we must divide the surface area of the cube by the surface area of the sphere.
ratio = (24_r_2)/(4_πr_2)
The _r_2 term cancels in the numerator and denominator. Also, 24/4 simplifes to 6.
ratio = (24_r_2)/(4_πr_2) = 6/π
The answer is 6/π.
← Didn't Know|Knew It →
What is the surface area of a hemisphere with a diameter of 4 cm?
What is the surface area of a hemisphere with a diameter of 4 cm?
Tap to reveal answer
A hemisphere is half of a sphere. The surface area is broken into two parts: the spherical part and the circular base.
The surface area of a sphere is given by SA = 4pi $r^{2}$.
So the surface area of the spherical part of a hemisphere is SA = 2pi $r^{2}$.
The area of the circular base is given by A = pi $r^{2}$. The radius to use is half the diameter, or 2 cm.
A hemisphere is half of a sphere. The surface area is broken into two parts: the spherical part and the circular base.
The surface area of a sphere is given by SA = 4pi $r^{2}$.
So the surface area of the spherical part of a hemisphere is SA = 2pi $r^{2}$.
The area of the circular base is given by A = pi $r^{2}$. The radius to use is half the diameter, or 2 cm.
← Didn't Know|Knew It →
A regular icosahedron has twenty congruent faces, each of which is an equilateral triangle.
The total surface area of a given regular icosahedron is 400 square centimeters. To the nearest tenth of a centimeter, what is the length of each edge?
A regular icosahedron has twenty congruent faces, each of which is an equilateral triangle.
The total surface area of a given regular icosahedron is 400 square centimeters. To the nearest tenth of a centimeter, what is the length of each edge?
Tap to reveal answer
The total surface area of the icosahedron is 400 square centimeters; since the icosahedron comprises twenty congruent faces, each has area  square centimeters.
square centimeters.
The area of an equilateral triangle is given by the formula

Set  and solve for
and solve for  :
:



 centimeters.
centimeters.
The total surface area of the icosahedron is 400 square centimeters; since the icosahedron comprises twenty congruent faces, each has area 
The area of an equilateral triangle is given by the formula
Set 


← Didn't Know|Knew It →
A regular octahedron has eight congruent faces, each of which is an equilateral triangle.
A given octahedron has edges of length five inches. Give the total surface area of the octahedron.
A regular octahedron has eight congruent faces, each of which is an equilateral triangle.
A given octahedron has edges of length five inches. Give the total surface area of the octahedron.
Tap to reveal answer
The area of an equilateral triangle is given by the formula

Since there are eight equilateral triangles that comprise the surface of the octahedron, the total surface area is

Substitute  :
:
 square inches.
square inches.
The area of an equilateral triangle is given by the formula
Since there are eight equilateral triangles that comprise the surface of the octahedron, the total surface area is
Substitute 

← Didn't Know|Knew It →
An upright cylinder with a height of 30 and a radius of 5 is in a big tub being filled with oil. If only the top 10% of the cylinder is visible, what is the surface area of the submerged cylinder?
An upright cylinder with a height of 30 and a radius of 5 is in a big tub being filled with oil. If only the top 10% of the cylinder is visible, what is the surface area of the submerged cylinder?
Tap to reveal answer
The height of the submerged part of the cylinder is 27cm. 2πrh + πr2 is equal to 270π + 25π = 295π
The height of the submerged part of the cylinder is 27cm. 2πrh + πr2 is equal to 270π + 25π = 295π
← Didn't Know|Knew It →
A right circular cylinder has a height of 41 in. and a lateral area (excluding top and bottom) 512.5π in2. What is the area of its bases?
A right circular cylinder has a height of 41 in. and a lateral area (excluding top and bottom) 512.5π in2. What is the area of its bases?
Tap to reveal answer
The lateral area (not including its bases) is equal to the circumference of the base times the height of the cylinder. Think of it like a label that is wrapped around a soup can. Therefore, we can write this area as:
A = h * π * d or A = h * π * 2r = 2πrh
Now, substituting in our values, we get:
512.5π = 2 * 41*rπ; 512.5π = 82rπ
Solve for r by dividing both sides by 82π:
6.25 = r
From here, we can calculate the area of a base:
A = 6.252π = 39.0625π
NOTE: The question asks for the area of the bases. Therefore, the answer is 2 * 39.0625π or 78.125π in2.
The lateral area (not including its bases) is equal to the circumference of the base times the height of the cylinder. Think of it like a label that is wrapped around a soup can. Therefore, we can write this area as:
A = h * π * d or A = h * π * 2r = 2πrh
Now, substituting in our values, we get:
512.5π = 2 * 41*rπ; 512.5π = 82rπ
Solve for r by dividing both sides by 82π:
6.25 = r
From here, we can calculate the area of a base:
A = 6.252π = 39.0625π
NOTE: The question asks for the area of the bases. Therefore, the answer is 2 * 39.0625π or 78.125π in2.
← Didn't Know|Knew It →
The diameter of the lid of a right cylindrical soup can is 5 in. If the can is 12 inches tall and the label costs $0.00125 per square inch to print, what is the cost to produce a label for a can? (Round to the nearest cent.)
The diameter of the lid of a right cylindrical soup can is 5 in. If the can is 12 inches tall and the label costs $0.00125 per square inch to print, what is the cost to produce a label for a can? (Round to the nearest cent.)
Tap to reveal answer
The general mechanics of this problem are simple. The lateral area of a right cylinder (excluding its top and bottom) is equal to the circumference of the top times the height of the cylinder. Therefore, the area of this can's surface is: 5π * 12 or 60π. If the cost per square inch is $0.00125, a single label will cost 0.00125 * 60π or $0.075π or approximately $0.24.
The general mechanics of this problem are simple. The lateral area of a right cylinder (excluding its top and bottom) is equal to the circumference of the top times the height of the cylinder. Therefore, the area of this can's surface is: 5π * 12 or 60π. If the cost per square inch is $0.00125, a single label will cost 0.00125 * 60π or $0.075π or approximately $0.24.
← Didn't Know|Knew It →
Aluminum is sold to a soup manufacturer at a rate of $0.0015 per square inch. The cans are made so that the ends perfectly fit on the cylindrical body of the can. It costs $0.00125 to attach the ends to the can. The outer label (not covering the top / bottom) costs $0.0001 per in2 to print and stick to the can. The label must be 2 inches longer than circumference of the can. Ignoring any potential waste, what is the manufacturing cost (to the nearest cent) for a can with a radius of 5 inches and a height of 12 inches?
Aluminum is sold to a soup manufacturer at a rate of $0.0015 per square inch. The cans are made so that the ends perfectly fit on the cylindrical body of the can. It costs $0.00125 to attach the ends to the can. The outer label (not covering the top / bottom) costs $0.0001 per in2 to print and stick to the can. The label must be 2 inches longer than circumference of the can. Ignoring any potential waste, what is the manufacturing cost (to the nearest cent) for a can with a radius of 5 inches and a height of 12 inches?
Tap to reveal answer
We have the following categories to consider:
= ( + ) * 0.0015
= 2 * 0.00125 = $0.0025
The area of ends of the can are each equal to π*52 or 25π. For two ends, that is 50π.
The lateral area of the can is equal to the circumference of the top times the height, or 2 * π * r * h = 2 * 5 * 12 * π = 120π.
Therefore, the total surface area of the aluminum can is 120π + 50π = 170π. The cost is 170π * 0.0015 = 0.255π, or approximately $0.80.
The area of the label is NOT the same as the lateral area of the can. (Recall that it must be 2 inches longer than the circumference of the can.) Therefore, the area of the label is (2 + 2 * π * 5) * 12 = (2 + 10π) * 12 = 24 + 120π. Multiply this by 0.0001 to get 0.0024 + 0.012π = (approximately) $0.04.
Therefore, the total cost is approximately 0.80 + 0.04 + 0.0025 = $0.8425, or $0.84.
We have the following categories to consider:
The area of ends of the can are each equal to π*52 or 25π. For two ends, that is 50π.
The lateral area of the can is equal to the circumference of the top times the height, or 2 * π * r * h = 2 * 5 * 12 * π = 120π.
Therefore, the total surface area of the aluminum can is 120π + 50π = 170π. The cost is 170π * 0.0015 = 0.255π, or approximately $0.80.
The area of the label is NOT the same as the lateral area of the can. (Recall that it must be 2 inches longer than the circumference of the can.) Therefore, the area of the label is (2 + 2 * π * 5) * 12 = (2 + 10π) * 12 = 24 + 120π. Multiply this by 0.0001 to get 0.0024 + 0.012π = (approximately) $0.04.
Therefore, the total cost is approximately 0.80 + 0.04 + 0.0025 = $0.8425, or $0.84.
← Didn't Know|Knew It →
The number of square units in the surface area of a right circular cylinder is equal to the number of cubic units in its volume. If r and h represent the length in units of the cylinder's radius and height, respectively, which of the following is equivalent to r in terms of h?
The number of square units in the surface area of a right circular cylinder is equal to the number of cubic units in its volume. If r and h represent the length in units of the cylinder's radius and height, respectively, which of the following is equivalent to r in terms of h?
Tap to reveal answer
We need to find expressions for the surface area and the volume of a cylinder. The surface area of the cylinder consists of the sum of the surface areas of the two bases plus the lateral surface area.
surface area of cylinder = surface area of bases + lateral surface area
The bases of the cylinder will be two circles with radius r. Thus, the area of each will be _πr_2, and their combined surface area will be 2_πr_2.
The lateral surface area of the cylinder is equal to the circumference of the circular base multiplied by the height. The circumferece of a circle is 2_πr_, and the height is h, so the lateral area is 2_πrh_.
surface area of cylinder = 2_πr_2 + 2_πrh_
Next, we need to find an expression for the volume. The volume of a cylinder is equal to the product of the height and the area of one of the bases. The area of the base is _πr_2, and the height is h, so the volume of the cylinder is πr_2_h.
volume = πr_2_h
Then, we must set the volume and surface area expressions equal to one another and solve for r in terms of h.
2_πr_2 + 2_πrh_ = πr_2_h
First, let's factor out 2_πr_ from the left side.
2_πr_(r + h) = πr_2_h
We can divide both sides by π.
2_r_(r + h) = r_2_h
We can also divide both sides by r, because the radius cannot equal zero.
2(r + h) = rh
Let's now distribute the 2 on the left side.
2_r_ + 2_h_ = rh
Subtract 2_r_ from both sides to get all the r's on one side.
2_h_ = rh – 2_r_
r_h – 2_r = 2_h_
Factor out an r from the left side.
r(h – 2) = 2_h_
Divide both sides by h – 2
r = 2_h_/(h – 2)
The answer is r = 2_h_/(h – 2).
We need to find expressions for the surface area and the volume of a cylinder. The surface area of the cylinder consists of the sum of the surface areas of the two bases plus the lateral surface area.
surface area of cylinder = surface area of bases + lateral surface area
The bases of the cylinder will be two circles with radius r. Thus, the area of each will be _πr_2, and their combined surface area will be 2_πr_2.
The lateral surface area of the cylinder is equal to the circumference of the circular base multiplied by the height. The circumferece of a circle is 2_πr_, and the height is h, so the lateral area is 2_πrh_.
surface area of cylinder = 2_πr_2 + 2_πrh_
Next, we need to find an expression for the volume. The volume of a cylinder is equal to the product of the height and the area of one of the bases. The area of the base is _πr_2, and the height is h, so the volume of the cylinder is πr_2_h.
volume = πr_2_h
Then, we must set the volume and surface area expressions equal to one another and solve for r in terms of h.
2_πr_2 + 2_πrh_ = πr_2_h
First, let's factor out 2_πr_ from the left side.
2_πr_(r + h) = πr_2_h
We can divide both sides by π.
2_r_(r + h) = r_2_h
We can also divide both sides by r, because the radius cannot equal zero.
2(r + h) = rh
Let's now distribute the 2 on the left side.
2_r_ + 2_h_ = rh
Subtract 2_r_ from both sides to get all the r's on one side.
2_h_ = rh – 2_r_
r_h – 2_r = 2_h_
Factor out an r from the left side.
r(h – 2) = 2_h_
Divide both sides by h – 2
r = 2_h_/(h – 2)
The answer is r = 2_h_/(h – 2).
← Didn't Know|Knew It →
What is the surface area of a cylinder with a radius of  and a height of
and a height of  ?
?
What is the surface area of a cylinder with a radius of 

Tap to reveal answer
When you're calculating the surface area of a cylinder, note that the cylinder will have two circles, one for the top and one for the bottom, and one rectangle that wraps around the "side" of the cylinder (it's helpful to picture peeling the label off a can of soup - it's curved when it's on the can, but really it's a rectangle that has been wrapped around). You know the area of the circle formula; for the rectangle, note that the height is given to you but the width of the rectangle is one you have to intuit: it's the circumference of the circle, because the entire distance around the circle from one point around and back again is the horizontal distance that the area must cover.
Therefore the surface area of a cylinder = 
When you're calculating the surface area of a cylinder, note that the cylinder will have two circles, one for the top and one for the bottom, and one rectangle that wraps around the "side" of the cylinder (it's helpful to picture peeling the label off a can of soup - it's curved when it's on the can, but really it's a rectangle that has been wrapped around). You know the area of the circle formula; for the rectangle, note that the height is given to you but the width of the rectangle is one you have to intuit: it's the circumference of the circle, because the entire distance around the circle from one point around and back again is the horizontal distance that the area must cover.
Therefore the surface area of a cylinder =
← Didn't Know|Knew It →
A circular swimming pool has diameter  meters and depth 5 meters throughout. Which of the following expressions gives the total surface area of the inside of the pool, in square meters?
meters and depth 5 meters throughout. Which of the following expressions gives the total surface area of the inside of the pool, in square meters?
A circular swimming pool has diameter 
Tap to reveal answer
The pool can be seen as a cylinder with depth (or height)  , and a base with diameter
, and a base with diameter  - and, subsequently, radius half this, or
- and, subsequently, radius half this, or  .
.
The swimming pool has one circular base, whose area is

The lateral side of the pool has area

Add these:

The pool can be seen as a cylinder with depth (or height) 


The swimming pool has one circular base, whose area is
The lateral side of the pool has area
Add these:
← Didn't Know|Knew It →
What is the lateral surface area of a cylinder with a base radius of  and a height of
and a height of  ?
?
What is the lateral surface area of a cylinder with a base radius of 

Tap to reveal answer
First, solve for circumference



The lateral surface area is equal to the circumference times the height. This gives us

First, solve for circumference
The lateral surface area is equal to the circumference times the height. This gives us
← Didn't Know|Knew It →
Consider a right, circular cylinder. The circular bases each have an area of  . If the height of the cylinder is
. If the height of the cylinder is  , then what is the lateral surface area of the cylinder?
, then what is the lateral surface area of the cylinder?
Consider a right, circular cylinder. The circular bases each have an area of 

Tap to reveal answer
The lateral surface area of a right circular cylinder is equal to the circumference of the base multiplied by the height.
If the base is a circle with area  , then the radius is
, then the radius is  , so
, so


Therefore, circumference times height gives us
 .
.
The lateral surface area of a right circular cylinder is equal to the circumference of the base multiplied by the height.
If the base is a circle with area 

Therefore, circumference times height gives us

← Didn't Know|Knew It →
The volume of a cylinder is 36π. If the cylinder’s height is 4, what is the cylinder’s diameter?
The volume of a cylinder is 36π. If the cylinder’s height is 4, what is the cylinder’s diameter?
Tap to reveal answer
Volume of a cylinder? V = πr2h. Rewritten as a diameter equation, this is:
V = π(d/2)2h = πd2h/4
Sub in h and V: 36p = πd2(4)/4 so 36p = πd2
Thus d = 6
Volume of a cylinder? V = πr2h. Rewritten as a diameter equation, this is:
V = π(d/2)2h = πd2h/4
Sub in h and V: 36p = πd2(4)/4 so 36p = πd2
Thus d = 6
← Didn't Know|Knew It →
