Complex Numbers - PSAT Math
Card 1 of 140
Simplify by rationalizing the denominator:

Simplify by rationalizing the denominator:
Tap to reveal answer
Multiply both numerator and denominator by  :
:








Multiply both numerator and denominator by 
← Didn't Know|Knew It →
Divide:

Divide:
Tap to reveal answer
Rewrite in fraction form, and multiply both numerator and denominator by  :
:








Rewrite in fraction form, and multiply both numerator and denominator by 
← Didn't Know|Knew It →
Simplify by rationalizing the denominator:

Simplify by rationalizing the denominator:
Tap to reveal answer
Multiply both numerator and denominator by  :
:








Multiply both numerator and denominator by 
← Didn't Know|Knew It →
Simplify by rationalizing the denominator:

Simplify by rationalizing the denominator:
Tap to reveal answer
Multiply the numerator and the denominator by the complex conjugate of the denominator, which is  :
:








Multiply the numerator and the denominator by the complex conjugate of the denominator, which is 
← Didn't Know|Knew It →
Simplify by rationalizing the denominator:

Simplify by rationalizing the denominator:
Tap to reveal answer
Multiply the numerator and the denominator by the complex conjugate of the denominator, which is  :
:








Multiply the numerator and the denominator by the complex conjugate of the denominator, which is 
← Didn't Know|Knew It →
Simplify by rationalizing the denominator:

Simplify by rationalizing the denominator:
Tap to reveal answer
Multiply the numerator and the denominator by the complex conjugate of the denominator, which is  :
:








Multiply the numerator and the denominator by the complex conjugate of the denominator, which is 
← Didn't Know|Knew It →
Define an operation  as follows:
as follows:
For all complex numbers  ,
,
 .
.
Evaluate  .
.
Define an operation 
For all complex numbers 

Evaluate 
Tap to reveal answer
← Didn't Know|Knew It →
Define an operation  as follows:
as follows:
For all complex numbers  ,
,
 .
.
Evaluate  .
.
Define an operation 
For all complex numbers 

Evaluate 
Tap to reveal answer





Multiply the numerator and the denominator by the complex conjugate of the denominator, which is  . The above becomes:
. The above becomes:







Multiply the numerator and the denominator by the complex conjugate of the denominator, which is 
← Didn't Know|Knew It →
Define an operation  as follows:
as follows:
For all complex numbers  ,
,

Evaluate  .
.
Define an operation 
For all complex numbers 
Evaluate 
Tap to reveal answer





Multiply the numerator and the denominator by the complex conjugate of the denominator, which is  . The above becomes:
. The above becomes:







Multiply the numerator and the denominator by the complex conjugate of the denominator, which is 
← Didn't Know|Knew It →
Which of the following is equal to  ?
?
Which of the following is equal to 
Tap to reveal answer

 , so 56 is a multiple of 4.
, so 56 is a multiple of 4.  raised to the power of any multiple of 4 is equal to 1, so
raised to the power of any multiple of 4 is equal to 1, so
 .
.



← Didn't Know|Knew It →
Multiply:

Multiply:
Tap to reveal answer
This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern

with 

This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern
with
← Didn't Know|Knew It →
Which of the following is equal to  ?
?
Which of the following is equal to 
Tap to reveal answer
By the power of a product property,

By the power of a product property,
← Didn't Know|Knew It →
Which of the following is equal to  ?
?
Which of the following is equal to 
Tap to reveal answer
The first step to solving this problem is distributing the exponent:

Next, we need simplify the complex portion.

Thus, our final answer is  .
.
The first step to solving this problem is distributing the exponent:
Next, we need simplify the complex portion.
Thus, our final answer is 
← Didn't Know|Knew It →
Simplify:

Simplify:
Tap to reveal answer
Use the FOIL method that states to multiply the Firsts, Outter, Inner, Lasts. Also remember that 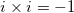 :
:

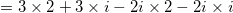


Use the FOIL method that states to multiply the Firsts, Outter, Inner, Lasts. Also remember that 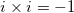
← Didn't Know|Knew It →
What is the eighth power of  ?
?
What is the eighth power of 
Tap to reveal answer



 raised to the power of any multiple of 4 is equal to 1, so the above expresion is equal to
raised to the power of any multiple of 4 is equal to 1, so the above expresion is equal to

This is not among the given choices.

This is not among the given choices.
← Didn't Know|Knew It →
What is the third power of  ?
?
What is the third power of 
Tap to reveal answer
You are being asked to evaluate

You can use the cube of a binomial pattern with  :
:






You are being asked to evaluate
You can use the cube of a binomial pattern with 
← Didn't Know|Knew It →
What is the fourth power of  ?
?
What is the fourth power of 
Tap to reveal answer
 can be calculated by squaring
can be calculated by squaring  , then squaring the result, using the square of a binomial pattern as follows:
, then squaring the result, using the square of a binomial pattern as follows:






![=\left [ \left (3 - i$\sqrt{2}$ \right $)^{2}$ \right $]^{2}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240822/gif.latex)








← Didn't Know|Knew It →
Multiply  by its complex conjugate. What is the product?
by its complex conjugate. What is the product?
Multiply 
Tap to reveal answer
The product of any complex number  and its complex conjugate
and its complex conjugate  is the real number
is the real number  , so all that is needed here is to evaluate the expression:
, so all that is needed here is to evaluate the expression:

The product of any complex number 


← Didn't Know|Knew It →
What is the eighth power of  ?
?
What is the eighth power of 
Tap to reveal answer
First, square  using the square of a binomial pattern as follows:
using the square of a binomial pattern as follows:




Raising this number to the fourth power yields the correct response:

![= \left [\left (1+ i \right $)^{2}$ \right $]^{4}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240868/gif.latex)



First, square 
Raising this number to the fourth power yields the correct response:
← Didn't Know|Knew It →
What is the ninth power of  ?
?
What is the ninth power of 
Tap to reveal answer


To raise a negative number to an odd power, take the absolute value of the base to that power and give its opposite:

To raise  to a power, divide the power by 4 and raise
to a power, divide the power by 4 and raise  to the remainder. Since
to the remainder. Since
 ,
,

Therefore,

To raise a negative number to an odd power, take the absolute value of the base to that power and give its opposite:
To raise 


Therefore,
← Didn't Know|Knew It →











