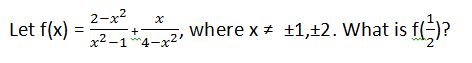Expressions - PSAT Math
Card 1 of 406
Which of the following phrases can be written as the algebraic expression 
?
Which of the following phrases can be written as the algebraic expression
Tap to reveal answer
is the cube of 
, which is the difference of a number and nineteen; therefore, 
is "the cube of the difference of a number and nineteen."
← Didn't Know|Knew It →
Which of the following phrases can be written as the algebraic expression 
?
Which of the following phrases can be written as the algebraic expression
Tap to reveal answer
is seventeen decreased by 
, which is the cube of a number; therefore, 
is "seventeen decreased by the cube of a number."
← Didn't Know|Knew It →
Increase 
by 70%. Which of the following will this be equal to?
Increase
Tap to reveal answer
A number increased by 70% is equivalent to 100% of the number plus 70% of the number. This is taking 170% of the number, or, equivalently, multiplying it by 1.7.
Therefore, 
increased by 70% is 1.7 times this, or
A number increased by 70% is equivalent to 100% of the number plus 70% of the number. This is taking 170% of the number, or, equivalently, multiplying it by 1.7.
Therefore,
← Didn't Know|Knew It →
Which of the following operations could represent the expression 
?
Which of the following operations could represent the expression
Tap to reveal answer
Begin by putting the equation given into your own words. It might sound something similar to:
2 times x squared plus 7
Now, go through each answer choice and see if any of them are similar to this. We immediately see that the answer "7 more than 2 times the square of x" is similar to what we came up with. Let's do a quick run through of the other choices to be sure of our choice:
"2 times 7 more than the square of x" is equal to 
, which is equivalent to 
.
"2 times 7 less than the square of x" is equal to 
, which is equivalent to 
.
"7 more than the square of 2x" is equal to 
, which is equivalent to 
.
"7 less than the square of 2x" is equal to 
, which is equivalent to 
.
The only answer that works is "7 more than 2 times the square of x". This is the correct answer.
Begin by putting the equation given into your own words. It might sound something similar to:
2 times x squared plus 7
Now, go through each answer choice and see if any of them are similar to this. We immediately see that the answer "7 more than 2 times the square of x" is similar to what we came up with. Let's do a quick run through of the other choices to be sure of our choice:
"2 times 7 more than the square of x" is equal to
"2 times 7 less than the square of x" is equal to
"7 more than the square of 2x" is equal to
"7 less than the square of 2x" is equal to
The only answer that works is "7 more than 2 times the square of x". This is the correct answer.
← Didn't Know|Knew It →
What does 
equal?
What does
Tap to reveal answer
When solving a complex expression, remember the acronym PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction). Reading left to right, begin by doing all operations within the innermost Parentheses first:
Continue simplifying using the acronym PEMDAS:
The expression is equal to -63.
When solving a complex expression, remember the acronym PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction). Reading left to right, begin by doing all operations within the innermost Parentheses first:
Continue simplifying using the acronym PEMDAS:
The expression is equal to -63.
← Didn't Know|Knew It →
If √(ab) = 8, and _a_2 = b, what is a?
If √(ab) = 8, and _a_2 = b, what is a?
Tap to reveal answer
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
Tap to reveal answer
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
← Didn't Know|Knew It →
what is 6/8 X 20/3
what is 6/8 X 20/3
Tap to reveal answer
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
← Didn't Know|Knew It →
Which of the following is equivalent to $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} ? Assume that denominators are always nonzero.
Which of the following is equivalent to $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} ? Assume that denominators are always nonzero.
Tap to reveal answer
We will need to simplify the expression $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We can think of this as a large fraction with a numerator of $\frac{1}{t}$-$\frac{1}{x}$ and a denominator of x-t.
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\frac{1}{t}$ has a denominator of t, and -$\frac{1}{x}$ has a denominator of x. The least common denominator that these two fractions have in common is xt. Thus, we are going to write equivalent fractions with denominators of xt.
In order to convert the fraction $\frac{1}{t}$ to a denominator with xt, we will need to multiply the top and bottom by x.
$\frac{1}{t}$=\frac{1cdot x}{tcdot x}$=\frac{x}{xt}$
Similarly, we will multiply the top and bottom of -$\frac{1}{x}$ by t.
$\frac{1}{x}$=\frac{1cdot t}{xcdot t}$=\frac{t}{xt}$
We can now rewrite $\frac{1}{t}$-$\frac{1}{x}$ as follows:
$\frac{1}{t}$-$\frac{1}{x}$ = $\frac{x}{xt}$-$\frac{t}{xt}$=\frac{x-t}{xt}$
Let's go back to the original fraction $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We will now rewrite the numerator:
$\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} = $\frac{frac{x-t}{xt}$}{x-t}
To simplify this further, we can think of $\frac{frac{x-t}{xt}$}{x-t} as the same as $\frac{x-t}{xt}$div (x-t) . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, adiv b=acdot $\frac{1}{b}$.
$\frac{x-t}{xt}$div (x-t) = $\frac{x-t}{xt}$cdot $\frac{1}{x-t}$=\frac{x-t}{xt(x-t)}$= $\frac{1}{xt}$
Lastly, we will use the property of exponents which states that, in general, $$\frac{1}{a}$=a^{-1}$.
$$\frac{1}{xt}$=(xt)^{-1}$
The answer is $(xt)^{-1}$.
We will need to simplify the expression $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We can think of this as a large fraction with a numerator of $\frac{1}{t}$-$\frac{1}{x}$ and a denominator of x-t.
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\frac{1}{t}$ has a denominator of t, and -$\frac{1}{x}$ has a denominator of x. The least common denominator that these two fractions have in common is xt. Thus, we are going to write equivalent fractions with denominators of xt.
In order to convert the fraction $\frac{1}{t}$ to a denominator with xt, we will need to multiply the top and bottom by x.
$\frac{1}{t}$=\frac{1cdot x}{tcdot x}$=\frac{x}{xt}$
Similarly, we will multiply the top and bottom of -$\frac{1}{x}$ by t.
$\frac{1}{x}$=\frac{1cdot t}{xcdot t}$=\frac{t}{xt}$
We can now rewrite $\frac{1}{t}$-$\frac{1}{x}$ as follows:
$\frac{1}{t}$-$\frac{1}{x}$ = $\frac{x}{xt}$-$\frac{t}{xt}$=\frac{x-t}{xt}$
Let's go back to the original fraction $\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t}. We will now rewrite the numerator:
$\frac{(frac{1}{t}$-$\frac{1}{x}$)}{x-t} = $\frac{frac{x-t}{xt}$}{x-t}
To simplify this further, we can think of $\frac{frac{x-t}{xt}$}{x-t} as the same as $\frac{x-t}{xt}$div (x-t) . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, adiv b=acdot $\frac{1}{b}$.
$\frac{x-t}{xt}$div (x-t) = $\frac{x-t}{xt}$cdot $\frac{1}{x-t}$=\frac{x-t}{xt(x-t)}$= $\frac{1}{xt}$
Lastly, we will use the property of exponents which states that, in general, $$\frac{1}{a}$=a^{-1}$.
$$\frac{1}{xt}$=(xt)^{-1}$
The answer is $(xt)^{-1}$.
← Didn't Know|Knew It →
Which of the following phrases can be written as the algebraic expression ?
Which of the following phrases can be written as the algebraic expression
Tap to reveal answer
is seventeen decreased by , which is the cube of a number; therefore, is "seventeen decreased by the cube of a number."
← Didn't Know|Knew It →
Increase by 70%. Which of the following will this be equal to?
Increase
Tap to reveal answer
A number increased by 70% is equivalent to 100% of the number plus 70% of the number. This is taking 170% of the number, or, equivalently, multiplying it by 1.7.
Therefore, increased by 70% is 1.7 times this, or
A number increased by 70% is equivalent to 100% of the number plus 70% of the number. This is taking 170% of the number, or, equivalently, multiplying it by 1.7.
Therefore,
← Didn't Know|Knew It →
Which of the following phrases can be written as the algebraic expression ?
Which of the following phrases can be written as the algebraic expression
Tap to reveal answer
is the cube of , which is the difference of a number and nineteen; therefore, is "the cube of the difference of a number and nineteen."
← Didn't Know|Knew It →
Which of the following operations could represent the expression ?
Which of the following operations could represent the expression
Tap to reveal answer
Begin by putting the equation given into your own words. It might sound something similar to:
2 times x squared plus 7
Now, go through each answer choice and see if any of them are similar to this. We immediately see that the answer "7 more than 2 times the square of x" is similar to what we came up with. Let's do a quick run through of the other choices to be sure of our choice:
"2 times 7 more than the square of x" is equal to , which is equivalent to .
"2 times 7 less than the square of x" is equal to , which is equivalent to .
"7 more than the square of 2x" is equal to , which is equivalent to .
"7 less than the square of 2x" is equal to , which is equivalent to .
The only answer that works is "7 more than 2 times the square of x". This is the correct answer.
Begin by putting the equation given into your own words. It might sound something similar to:
2 times x squared plus 7
Now, go through each answer choice and see if any of them are similar to this. We immediately see that the answer "7 more than 2 times the square of x" is similar to what we came up with. Let's do a quick run through of the other choices to be sure of our choice:
"2 times 7 more than the square of x" is equal to
"2 times 7 less than the square of x" is equal to
"7 more than the square of 2x" is equal to
"7 less than the square of 2x" is equal to
The only answer that works is "7 more than 2 times the square of x". This is the correct answer.
← Didn't Know|Knew It →
What does equal?
What does
Tap to reveal answer
When solving a complex expression, remember the acronym PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction). Reading left to right, begin by doing all operations within the innermost Parentheses first:
Continue simplifying using the acronym PEMDAS:
The expression is equal to -63.
When solving a complex expression, remember the acronym PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction). Reading left to right, begin by doing all operations within the innermost Parentheses first:
Continue simplifying using the acronym PEMDAS:
The expression is equal to -63.
← Didn't Know|Knew It →
A rowing team paddles upstream at a rate of 10 miles every 2 hours and downstream at a rate of 27 miles every 3 hours. Assuming they are paddling at the same rate up and downstream, what is the speed of the water?
A rowing team paddles upstream at a rate of 10 miles every 2 hours and downstream at a rate of 27 miles every 3 hours. Assuming they are paddling at the same rate up and downstream, what is the speed of the water?
Tap to reveal answer
Upstream: p – w = (10/2) or p – w = 5 miles/hour
Downstream: p + w = (27/3) or p + w = 9 miles/hour
Then we add the two equations together to cancel out the w's. After adding we see
2p = 14
p = 7 miles/hour where p is the rate of the paddling. We plug p into the equation to find
w = 2 miles/hour where w is the rate of the stream's water.
Upstream: p – w = (10/2) or p – w = 5 miles/hour
Downstream: p + w = (27/3) or p + w = 9 miles/hour
Then we add the two equations together to cancel out the w's. After adding we see
2p = 14
p = 7 miles/hour where p is the rate of the paddling. We plug p into the equation to find
w = 2 miles/hour where w is the rate of the stream's water.
← Didn't Know|Knew It →
If ab - bc + d = d2 - c2, then what is the value of a when b is two, c is negative one, and d is zero?
If ab - bc + d = d2 - c2, then what is the value of a when b is two, c is negative one, and d is zero?
Tap to reveal answer
ab - bc + d = d2 - c2
We need to substitute values in for b, c, and d, and then solve the equation for a.
a(2) - 2(-1) + 0 = 02 - (-1)2
2a +2 + 0 = 0 - (1)
2a + 2 = -1
2a = -3
a = -3/2
The answer is -3/2.
ab - bc + d = d2 - c2
We need to substitute values in for b, c, and d, and then solve the equation for a.
a(2) - 2(-1) + 0 = 02 - (-1)2
2a +2 + 0 = 0 - (1)
2a + 2 = -1
2a = -3
a = -3/2
The answer is -3/2.
← Didn't Know|Knew It →
If 11x + 4 = 19x – 12, then what is 2x – 4?
If 11x + 4 = 19x – 12, then what is 2x – 4?
Tap to reveal answer
First solve for x. The first equation would simplify as:
16 = 8x
x = 2
If we plug x = 2 into the second expression:
2(2) – 4 = 0
0 is the correct answer.
First solve for x. The first equation would simplify as:
16 = 8x
x = 2
If we plug x = 2 into the second expression:
2(2) – 4 = 0
0 is the correct answer.
← Didn't Know|Knew It →
If x = 2 and y = 3, then evaluate 2(x – 3) + 5y2
If x = 2 and y = 3, then evaluate 2(x – 3) + 5y2
Tap to reveal answer
To evaluate an expression we make substitutions into the expression
2(x – 3) + 5y2 becomes 2(2 – 3) + 5 * 32 = –2 + 45 = 43
To evaluate an expression we make substitutions into the expression
2(x – 3) + 5y2 becomes 2(2 – 3) + 5 * 32 = –2 + 45 = 43
← Didn't Know|Knew It →
IF 5x3 = 40, then what is the value of 12x – (x/2)?
IF 5x3 = 40, then what is the value of 12x – (x/2)?
Tap to reveal answer
Use the first equation to solve for x, then plug into the 2nd equation to find a value.
5x3 = 40
x3 = 8
x = 2
12(2) – (2/2) = 24 – 1 = 23
Use the first equation to solve for x, then plug into the 2nd equation to find a value.
5x3 = 40
x3 = 8
x = 2
12(2) – (2/2) = 24 – 1 = 23
← Didn't Know|Knew It →