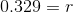Pre-Calculus - Application Problems

The exponential decay of an element is given by the following function:

$Q(t)=Q_0e^{-0.04223t}$

Where is the amount of the element left after days, and is the initial amount of the element. If there are kg of the element left after days, what was the initial amount of the element?

Explanation

The problem asks us for the initial amount of the element, so first let's solve our equation for :

$Q(t)=Q_0e^{-0.04223t}$

$Q_0=Q(t)e^{0.04223t}$

The problem tells us that 25 days has passed, which gives us , and it also tells us the amount left after 25 days, which gives us . Now that we have our equation for , we can plug in the given values to find the initial amount of the element:

$Q_0=Q(25)e^{0.04223(25)}=(37)e^{0.04223(25)}=106.3$ kg

If you deposit into a savings account which earns a yearly interest rate, how much is in your account after two years?

$$\small 110.25$

Explanation

Since we are investing for two years with a yearly rate of 5%, we will use the formula to calculate compound interest.

where

is the amount of money after time.

is the principal amount (initial amount).

is the interest rate.

is time.

Our amount after two years is:

$\small 100(1.05^2)=100(1.1025)=110.25$

If you deposit into a savings account which compounds interest every month, what is the expression for the amount of money in your account after years if you earn a nominal interest rate of compounded monthly?

$\small R\bigg(1+\frac{i}{12}\bigg)^{24}$

$\small \small R\bigg(1+\frac{i}{12}\bigg)^{2}$

$\small \small R\big(1+i\big)^{2}$

$\small \small R\big(1+i\big)^{24}$

Explanation

Since is the nominal interest rate compounded monthly we write the interest term as $\frac{i}{12}$ as it is the effective monthly rate.

We compound for years which is months. Since our interest rate is compounded monthly our time needs to be in the same units thus, months will be the units of time.

Plugging this into the equation for compound interest gives us the expression:

$A=P\left(1+\frac{i}{c}\right)^{ct}$

$A=R\left(1+\frac{i}{12}\right)^{12\cdot 2}$

$A=\small \small R \left(1+\frac{i}{12}\right)^{24}$

Stuff animals were a strange craze of the 90's. A Cat stuff animal with white paws sold for $6 in 1997. In 2015, the Cat will sell for $1015. What has been the approximate rate of growth for these stuff animal felines?

Explanation

Use the formula for exponential growth where y is the current value, A is the initial value, r is the rate of growth, and t is time. Between 1997 and 2015, 18 years passed, so use . The stuffed animal was originally worth $6, so . It is now worth $1,015, so .

Our equation is now:

$1015 = 6*(1+r)^{18}$ divide by 6:

$169.1\overline{6}=(1+r)^{18}$ take both sides to the power of $\frac{1}{18}=0.0\overline{5}$ :

$1.329 \approx 1+r$ subtract 1

As a percent, r is about 33%.

Suppose you took out a loan years ago that gains interest. Suppose that you haven't made any payments on it yet, and right now you owe on the loan. How much was the loan worth when you took it out?

None of the other answers.

Explanation

The formula for the compund interest is as follows:

By substuting known values into the compound interest formula, we have:

$100000 = P(1.069)^{10}$ .

From here, substitute known values.

$\frac{100000}{1.069^{10}} = P$

Divide by $1.069^{10}$

There were 240mg of caffeine in the discontinued energy drink. The decay rate for caffeine in the human bloodstream is around 0.14. If Jackie drinks this energy drink around 8PM, how much caffeine will still be in her system at midnight?

Explanation

Because this is a process taking place in the human body, we should use the exponential decay formula involving e:

$A=P*e^{rt}$

where A is the current amount, P is the initial amount, r is the rate of growth/decay, and t is time.

In this case, since the amount of caffeine is decreasing rather than increasing, use . Between 8PM and midnight, 4 hours pass, so use . The initial amount of caffeine is given as 240 mg, so use .

Now evaluate:

$\ A = 240\cdot e^{-0.14\cdot 4} \ \= 240\cdot e^{-0.56} \approx 240 \cdot 0.57 \ \= 137.1$

The exponential decay of an element is given by the function

$Q(t) = Q_o e^{-0.9t}$

In this function, is the amount left after days, and is the initial amount of the element. What percent of the element is left after ten days, rounded to the nearest whole percent?

Explanation

To find the final percentage of the element left, we must rearrange the equation to solve for $e^{-0.9t}$ :

$\frac{Q(t)}{Q_o} = e^{-0.9t}$

Now, using the ten days as , we can solve for the percent of the element left after ten days:

$\frac{Q(10)}{Q_o} = e^{-0.9*10} \approx 0.0001 = 0.01% \approx 0%$

The exponential decay of an element is given by the function

$Q(t) = Q_o e^{-0.0327t}$

where is the amount of the element after days, and is the initial amount of the element. If of the element are left after four days, how much of the element was there initially, to the nearest tenth of a kilogram?

Explanation

To solve for the initial amount, we must use rearrange the equation:

$Q_o = \frac{Q(t)}{e^{-0.0327t}}$

We now substitute the values given from the problem

$Q_o = \frac{Q(4)}{e^{-0.0327*4}} = \frac{3}{e^{-0.0327*4}} = 3.4:kg$

The exponential decay of an element is given by the function:

$Q(t) = Q_oe^{-0.42t}$

In this function, is the amount of the element left after days, and is the initial amount of the element. If of the element is left after seven days, how much of the element was there to begin with, rounded to the nearest kilogram?

Explanation

To find the initial amount, you must rearrange the equation to solve for :

$Q(t) = Q_oe^{-0.42t}$

Divide both sides by $e^{-0.42t}$ :

$Q_o = \frac{Q(t)}{e^{-0.42t}}$

Substituting in the values from the problem gives

$Q_o = \frac{25}{e^{-0.42(7)}} \approx 473:kg$

John opens a savings account and deposits into it. This savings account gains interest per year. After years, John withdraws all the money, and deposits it into another savings account with interest per year. years later, John withdraws the money.