Graphs - Pre-Calculus
Card 1 of 4
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by  and
and 
Then by Hardy-Weinberg:
 , where both
, where both  and
and  are non-negative.
are non-negative.
Which statement discribes the graph that would appropriately represents the above relation?
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by 
Then by Hardy-Weinberg:



Which statement discribes the graph that would appropriately represents the above relation?
Tap to reveal answer
The equation can be reduced by taking the square root of both sides.


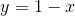
As a simple test, all other values when substituted into the original equation fail. However,  works. Therefore
works. Therefore  is our answer.
is our answer.
The equation can be reduced by taking the square root of both sides.
As a simple test, all other values when substituted into the original equation fail. However, 

← Didn't Know|Knew It →
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by  and
and 
Then by Hardy-Weinberg:
 , where both
, where both  and
and  are non-negative.
are non-negative.
Which statement discribes the graph that would appropriately represents the above relation?
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by 
Then by Hardy-Weinberg:



Which statement discribes the graph that would appropriately represents the above relation?
Tap to reveal answer
The equation can be reduced by taking the square root of both sides.


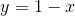
As a simple test, all other values when substituted into the original equation fail. However,  works. Therefore
works. Therefore  is our answer.
is our answer.
The equation can be reduced by taking the square root of both sides.
As a simple test, all other values when substituted into the original equation fail. However, 

← Didn't Know|Knew It →
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by  and
and 
Then by Hardy-Weinberg:
 , where both
, where both  and
and  are non-negative.
are non-negative.
Which statement discribes the graph that would appropriately represents the above relation?
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by 
Then by Hardy-Weinberg:



Which statement discribes the graph that would appropriately represents the above relation?
Tap to reveal answer
The equation can be reduced by taking the square root of both sides.


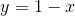
As a simple test, all other values when substituted into the original equation fail. However,  works. Therefore
works. Therefore  is our answer.
is our answer.
The equation can be reduced by taking the square root of both sides.
As a simple test, all other values when substituted into the original equation fail. However, 

← Didn't Know|Knew It →
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by  and
and 
Then by Hardy-Weinberg:
 , where both
, where both  and
and  are non-negative.
are non-negative.
Which statement discribes the graph that would appropriately represents the above relation?
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by 
Then by Hardy-Weinberg:



Which statement discribes the graph that would appropriately represents the above relation?
Tap to reveal answer
The equation can be reduced by taking the square root of both sides.


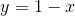
As a simple test, all other values when substituted into the original equation fail. However,  works. Therefore
works. Therefore  is our answer.
is our answer.
The equation can be reduced by taking the square root of both sides.
As a simple test, all other values when substituted into the original equation fail. However, 

← Didn't Know|Knew It →