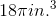Pre-Algebra - Volume of a Sphere

Michelle plays softball for her high school. She is the only pitcher on the team. She is the only player that is guaranteed to touch the ball on every play. The problem is, her hands are not big enough to get a grip on the ball because the ball is too big. What is the volume of the softball that has a diameter of 6 inches?

$36 \pi inches^3$

$288\pi inches^3$

$36\pi inches^2$

$288\pi inches^2$

$48\pi inches^3$

Explanation

The formula to find the volume of a sphere is $\frac{4}{3} * \pi * r^3$

Find the radius of the softball and substitute that in place of r.

Answer will be left in pi format.

$36\pi inches^3$

A sphere has diameter 3 meters. Give its volume in cubic centimeters (leave in terms of $\pi$ ).

$4,500,000\pi \textrm{ cm}^{3}$

$1,125,000\pi \textrm{ cm}^{3}$

$3,375,000\pi \textrm{ cm}^{3}$

$27,000,000\pi \textrm{ cm}^{3}$

$36,000,000\pi \textrm{ cm}^{3}$

Explanation

The diameter of 3 meters is equal to $3 \times 100 = 300$ centimeters; the radius is half this, or 150 centimeters. Substitute in the volume formula:

$V= \frac{4}{3} \pi r^{3}$

$V= \frac{4}{3} \cdot \pi \cdot 150^{3}$

$V= \frac{4}{3} \cdot 150 \cdot 150 \cdot 150\cdot \pi$

$V= 4,500,000\pi$ cubic centimeters

A certain children's basketball has a diameter of 6 inches. What is the volume of the basketball?

$36\pi in.^{3}$

$108\pi in.^{3}$

$288\pi in.^{3}$

$9\pi in.^{3}$

$18\pi in.^{3}$

Explanation

Math involves a lot of formulas. Unfortunately that means we either have to do some memorization or compile a really long list of formulas for reference. Either way, a basketball is a sphere, which means we have to know the formula for the volume of a sphere to solve this problem.

$V=\frac{4}{3}\pi r^{3}$

stands for volume, and stands for radius. Therefore, all we need to do is plug in the radius of the basketball and do a little calculation to find our answer. The problem is that we do not have the radius. All we have is a diameter. But if we remember the relationship between diameters and radii (the plural of radius), we have nothing to fear. The diameter is just twice as long as the radius. That means that if our diameter is 6 inches, the radius is simply 3 inches. Now that we have our radius, we are ready to plug and play.

$V=\frac{4}{3}\pi (3)^{3}=\frac{4}{3}\pi(27)=36\pi$

Since our original unit was inches, and volume is always expressed in cubic units, our final answer is

$36\pi in.^3$

Find the volume of a sphere with a diameter of .

$\frac{500}{3}\pi$

$500\pi$

$375\pi$

$\frac{100}{3}\pi$

$\frac{400}{3}\pi$

Explanation

Write the formula to find the volume of a sphere.

$V=\frac{4}{3}\pi r^3$

Divide the diameter by two to obtain the radius. The radius is five.

Substitute the radius into the volume equation.

$V=\frac{4}{3}\pi (5)^3=\frac{4}{3}\pi (125) = \frac{500}{3}\pi$

In terms of $\pi$ , give the volume, in cubic inches, of a spherical water tank with a diameter of 20 feet.

$2,304,000 \pi \textrm{ in}^{3}$

$18,432,000\pi\textrm{ in}^{3}$

$57,600 \pi\textrm{ in}^{3}$

$230,400 \pi\textrm{ in}^{3}$

$307,200\pi\textrm{ in}^{3}$

Explanation

20 feet = $20 \times 12 = 240$ inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set , substitute in the volume formula, and solve for :

$V = \frac{4}{3} \pi r^{3}$

$V = \frac{4}{3} \pi \cdot 120^{3}$

$V = \frac{4}{3} \pi \cdot 1,728,000$

$V = 2,304,000 \pi$ cubic inches

Regulations for professional soccer state that the diameter of the ball must be 8.65 inches for a size 5 regulation ball. What is the volume of the soccer ball?

The answer is not present.

Explanation

The volume of a sphere is given by $\frac{4}{3}\pi r^3$ . The problem listed the diameter of the ball. Half of this number is the radius.

$V=\frac{4}{3}\pi (4.325)^3=339in^3$

When using a calculator to solve these types of problems it is best to do the problem in chunks to avoid input errors. For instance find out what the value of the radius cubed is first. Then multiply the other terms.

The units of volume are always cubed, not squared.

A hollow sphere has a diameter of 8 inches from the center of the sphere to the outermost shell. The shell of the sphere is 1 inch thick. What is the volume of the shell or wall of the sphere?

Explanation

The questions asks the volume of the wall of the sphere only. Therefore it is necessary to find the total volume of the large sphere and subtract the volume of the inner sphere (formed by the wall) from it.

Volume of large sphere:

$V=\frac{4}{3} \pi r^3=\frac{4}{3}\pi(4^3)=268.1in^3$