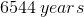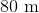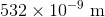Quantum and Nuclear Physics
Help Questions
Physics › Quantum and Nuclear Physics
A monochromatic light source is incident on a neutral density filter which decreases the light source's intensity by a factor of 3 but does not change its color. What happens to the energy of a photon in the less intense beam?
None of these
The photon energy decreases by a factor of 3.
The photon energy increases by a factor of 3.
The photon energy decreases by a factor of 9.
The photon energy decreases only slightly.
Explanation
The photon energy does not change since the color of light (and therefore the frequency of the light) does not change.
Radiocarbon dating is a method that allows scientists to estimate the age of organisms after they have died. A fairly constant amount of radioactive 




If a scientist finds that a fossil contains 

Explanation
In this question, we're given a brief description of radiocarbon dating. We're given the amount of 
First, let's briefly go over radiocarbon dating. This method essentially assumes that the amount of radioactive carbon within an organism remains fairly stable at any given time while the organism is alive. Moreover, this amount of radioactive carbon is related to the amount of radioactive carbon in the atmosphere. Once the organism dies, however, it ceases to gain any radioactive carbon; rather, the 


Since we're dealing with the decay of 
We can further rearrange this expression to isolate the variable for time.
In arriving at this expression, we see that we need to know the rate constant, 

Rearranging, we can find the rate-constant.
Now that we have the rate constant, we can plug this value into the previous expression to solve for 
Radiocarbon dating is a method that allows scientists to estimate the age of organisms after they have died. A fairly constant amount of radioactive 




If a scientist finds that a fossil contains 

Explanation
In this question, we're given a brief description of radiocarbon dating. We're given the amount of 
First, let's briefly go over radiocarbon dating. This method essentially assumes that the amount of radioactive carbon within an organism remains fairly stable at any given time while the organism is alive. Moreover, this amount of radioactive carbon is related to the amount of radioactive carbon in the atmosphere. Once the organism dies, however, it ceases to gain any radioactive carbon; rather, the 


Since we're dealing with the decay of 
We can further rearrange this expression to isolate the variable for time.
In arriving at this expression, we see that we need to know the rate constant, 

Rearranging, we can find the rate-constant.
Now that we have the rate constant, we can plug this value into the previous expression to solve for 
A car with mass 

Explanation
The de Broglie wavelength is given by 
A monochromatic light source is incident on a neutral density filter which decreases the light source's intensity by a factor of 3 but does not change its color. What happens to the energy of a photon in the less intense beam?
None of these
The photon energy decreases by a factor of 3.
The photon energy increases by a factor of 3.
The photon energy decreases by a factor of 9.
The photon energy decreases only slightly.
Explanation
The photon energy does not change since the color of light (and therefore the frequency of the light) does not change.
A monochromatic light source is incident on a neutral density filter which decreases the light source's intensity by a factor of 3 but does not change its color. What happens to the energy of a photon in the less intense beam?
None of these
The photon energy decreases by a factor of 3.
The photon energy increases by a factor of 3.
The photon energy decreases by a factor of 9.
The photon energy decreases only slightly.
Explanation
The photon energy does not change since the color of light (and therefore the frequency of the light) does not change.
A car with mass 

Explanation
The de Broglie wavelength is given by 
Radiocarbon dating is a method that allows scientists to estimate the age of organisms after they have died. A fairly constant amount of radioactive 




If a scientist finds that a fossil contains 

Explanation
In this question, we're given a brief description of radiocarbon dating. We're given the amount of 
First, let's briefly go over radiocarbon dating. This method essentially assumes that the amount of radioactive carbon within an organism remains fairly stable at any given time while the organism is alive. Moreover, this amount of radioactive carbon is related to the amount of radioactive carbon in the atmosphere. Once the organism dies, however, it ceases to gain any radioactive carbon; rather, the 


Since we're dealing with the decay of 
We can further rearrange this expression to isolate the variable for time.
In arriving at this expression, we see that we need to know the rate constant, 

Rearranging, we can find the rate-constant.
Now that we have the rate constant, we can plug this value into the previous expression to solve for 
A car with mass 

Explanation
The de Broglie wavelength is given by 
A laser outputs light of a single color with photon energy 
Explanation
Halving the wavelength is equivalent to doubling the frequency since for a light wave the wavelength and frequency are related by