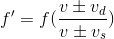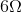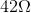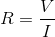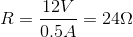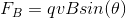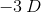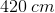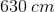Electromagnetics, Waves, and Optics
Help Questions
Physics › Electromagnetics, Waves, and Optics
Suppose that car A and car B are both traveling in the same direction. Car A is going 


Note: The speed of sound in air is 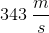
Explanation
The important concept being tested in this question is the Doppler effect. When a source of sound waves (or any other wave) is emitted from a source and is moving relative to some observer, the actual frequency of the wave will be different for the observer.
For starters, we'll need to use the Doppler equation.
The trickiest part about this question is to decide whether to add or subtract in both the numerator and denominator. To find the right sign orientation, it's helpful to do a quick thought experiment. Imagine that only one of them is moving and the other is stationary. Decide how that will affect the observed frequency; will it increase it or decrease it? Then repeat for the other one.
First, let's consider the detector (aka observer). We're told that car B, the detector, is traveling ahead of car A and also in the same direction. This means that car B is driving away from car A. So in this situation, is the frequency that car B hears expected to increase or decrease? The answer is that it will decrease. Since car B is traveling away from car A, each successive wave will take longer to reach car B. Hence, we will use subtraction in the numerator because that will make the observed frequency smaller.
Now let's apply this same logic to the denominator, which deals with the source of the sound waves. We know that car A is traveling in the same direction as car B and is behind. This means that car A is traveling toward car B. So from this perspective, each successive wave is expected to get closer together, thus making the time between each wave smaller and the frequency bigger. In the denominator, will adding or subtracting make the observed frequency bigger? The answer is subtraction. By making a smaller number in the denominator, the entire fraction becomes larger.
Keeping this information in mind, we'll need to use subtraction in both the numerator and denominator. Once we plug in the values given in the question stem, we have everything we need to solve for the answer.
A conductor is placed in an electric field under electrostatic conditions. Which of the following statements is correct for this situation?
All of these
The electric field is zero inside the conductor
All valence electrons go to the surface of the conductor
The electric field on the surface of the conductor is perpendicular to the surface
Explanation
A conductor is defined as a object free to move charges. In particular, valence electrons, which are the outer most electron in each atom and the most free to move, travel inside the conductor until the net electric field inside the conductor is zero. These electrons will move until this condition has been met. Because of the presents of charged particles at the surface and the condition that they are no longer moving, any electric field at the surface must be perpendicular to that surface.

Three equal charges are at three of the corners of a square of side d. A fourth charge of equal magnitude is at the center of the square as shown in Figure above. Which of the arrows shown represents the net force acting on the charge at the center of the square?
B
A
C
D
Explanation
Because of the principles of superposition, each electric force that acts from the charges at the corners on to the charge at the center can be broken into components. Since all the charges are positive, all the forces will be repulsive. The forces acting from the top left and bottom right corners will cancel, leaving only the repulsive force coming from the bottom left corner.
What size resistor should be connected across the terminals of a 

Explanation
Ohm's law is 
In this case, 

Solving for the resistance, 
Substitute known values and solve for the unknown resistance:
A single string of wire has a resistance of 

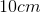
Explanation
So this is all about the magnetic field strength around a current carrying wire.
The equation for this is:
But you must use Ohm's Law 
Since the wire has 


Being sure to change 

Suppose that car A and car B are both traveling in the same direction. Car A is going 


Note: The speed of sound in air is 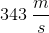
Explanation
The important concept being tested in this question is the Doppler effect. When a source of sound waves (or any other wave) is emitted from a source and is moving relative to some observer, the actual frequency of the wave will be different for the observer.
For starters, we'll need to use the Doppler equation.
The trickiest part about this question is to decide whether to add or subtract in both the numerator and denominator. To find the right sign orientation, it's helpful to do a quick thought experiment. Imagine that only one of them is moving and the other is stationary. Decide how that will affect the observed frequency; will it increase it or decrease it? Then repeat for the other one.
First, let's consider the detector (aka observer). We're told that car B, the detector, is traveling ahead of car A and also in the same direction. This means that car B is driving away from car A. So in this situation, is the frequency that car B hears expected to increase or decrease? The answer is that it will decrease. Since car B is traveling away from car A, each successive wave will take longer to reach car B. Hence, we will use subtraction in the numerator because that will make the observed frequency smaller.
Now let's apply this same logic to the denominator, which deals with the source of the sound waves. We know that car A is traveling in the same direction as car B and is behind. This means that car A is traveling toward car B. So from this perspective, each successive wave is expected to get closer together, thus making the time between each wave smaller and the frequency bigger. In the denominator, will adding or subtracting make the observed frequency bigger? The answer is subtraction. By making a smaller number in the denominator, the entire fraction becomes larger.
Keeping this information in mind, we'll need to use subtraction in both the numerator and denominator. Once we plug in the values given in the question stem, we have everything we need to solve for the answer.
Suppose that a magnetic field is oriented such that it is pointing directly to the left, as in the picture shown below. If a positively charged particle were to begin traveling through this magnetic field to the right, in which direction would the particle's trajectory begin to curve?

The particle would continue to move to the right unaffected
The particle would move out of the page
The particle would move down the page
The particle would move into the page
Explanation
In order to answer this question, it's important to understand the factors that determine the magnetic force experienced by a charge. We can begin by writing out the equation for magnetic force.
As shown in the above equation, the magnetic force is directly proportional to the particle's charge, its velocity, and the strength of the magnetic field itself. But, for the purposes of the this question, the most important factor is the angle of the particle's velocity with respect to the magnetic field.
Notice that if theta is equal to zero, then the sine of theta will be equal to zero as well. This, in turn, will cause the magnetic force to also be zero. This is also true if we were to define theta as 
Since the particle is moving in a direction that is parallel to the magnetic field lines but in the opposite direction, we have a situation in which theta is equal to 
Suppose that a magnetic field is oriented such that it is pointing directly to the left, as in the picture shown below. If a positively charged particle were to begin traveling through this magnetic field to the right, in which direction would the particle's trajectory begin to curve?

The particle would continue to move to the right unaffected
The particle would move out of the page
The particle would move down the page
The particle would move into the page
Explanation
In order to answer this question, it's important to understand the factors that determine the magnetic force experienced by a charge. We can begin by writing out the equation for magnetic force.
As shown in the above equation, the magnetic force is directly proportional to the particle's charge, its velocity, and the strength of the magnetic field itself. But, for the purposes of the this question, the most important factor is the angle of the particle's velocity with respect to the magnetic field.
Notice that if theta is equal to zero, then the sine of theta will be equal to zero as well. This, in turn, will cause the magnetic force to also be zero. This is also true if we were to define theta as 
Since the particle is moving in a direction that is parallel to the magnetic field lines but in the opposite direction, we have a situation in which theta is equal to 
For most people, the nearest distance that objects can be located away from the eye and still seen clearly is 



Explanation
For this question, we're given the definition of near point. We're told what the near point is in the average person, and also the near point for a certain person who can't see well and needs glasses. We're asked to find the refractive power of a lens that will bring this individual's near point to the average, healthy value.
As was stated in the question stem, the near point is the closest distance of an object from the eye where that object can still be seen clearly. In the question, we're told that the normal value for this is 

The idea is to be able to make the individual see things clearly when objects are located 


With this information in hand, we can use the lens-makers equation to solve for the refractive power of the lens.
We know that the object will be located a distance of 


Also, remember that to find refractive power, we'll need to have our units be in meters.
Furthermore, recall that refractive power is equal to the inverse of focal length.
Hence, the power of the refractive lens will need to be 
Suppose that the fifth harmonic of a standing wave contained within a pipe closed at both ends has a wavelength of 
Explanation
For this question, we're told that a standing wave is contained within a pipe closed at both ends. We're also given the wavelength for the fifth harmonic, and are asked to find the length of the pipe.
The first step to solve this problem is to use the equation for a pipe closed at both ends.
Since we're told which harmonic the wave is on, as well as its wavelength, we have everything we need to solve for the length of the pipe.