Optics - MCAT Chemical and Physical Foundations of Biological Systems
Card 1 of 224
A light ray traveling through a medium is reflected by a second medium at an angle of 20⁰ to the interface between the two media. Which of the following is true?
A light ray traveling through a medium is reflected by a second medium at an angle of 20⁰ to the interface between the two media. Which of the following is true?
Tap to reveal answer
The angle of reflection is the angle between the reflected light ray and a line perpendicular to the interface between the two media. The angle of reflection must be complementary to 20o.
90o – 20o = 70⁰
The angle of reflection is the angle between the reflected light ray and a line perpendicular to the interface between the two media. The angle of reflection must be complementary to 20o.
90o – 20o = 70⁰
← Didn't Know|Knew It →
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
The process of light entering glass from the air is called .
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
The process of light entering glass from the air is called .
Tap to reveal answer
This question is asking us about the different processes that can happen to light upon hitting a surface. Thinking back to the properties of light, we know that absorption, reflection, and refraction are all processes that light can undergo when interacting with a surface.
Absorption means that the energy associated with the light is captured, and no photons are ejected from the surface after the collision of the incident photon and the surface. Reflection occurs when no light enters the new medium and instead bounces off at the angle to normal that it hit. Refraction occurs when some light enters the new medium. In this case, light is entering glass from the air; thus, the process we are concerned about is refraction.
This question is asking us about the different processes that can happen to light upon hitting a surface. Thinking back to the properties of light, we know that absorption, reflection, and refraction are all processes that light can undergo when interacting with a surface.
Absorption means that the energy associated with the light is captured, and no photons are ejected from the surface after the collision of the incident photon and the surface. Reflection occurs when no light enters the new medium and instead bounces off at the angle to normal that it hit. Refraction occurs when some light enters the new medium. In this case, light is entering glass from the air; thus, the process we are concerned about is refraction.
← Didn't Know|Knew It →
Sound projected from an opera stage strikes a flat wall in the opera house at an angle 
to the normal. What conclusion can be drawn about the reflection of this sound from the wall back into the room?
Sound projected from an opera stage strikes a flat wall in the opera house at an angle
Tap to reveal answer
For all waves, the angle of incidence is equal to the angle of reflection. The projection is to the opposite side of the normal at the same angle as the incident wave.
Think of the wall as a mirror. The angle with which the wave impacts a mirror will be equal to the angle with which it is reflected, but mirrored across the normal.
For all waves, the angle of incidence is equal to the angle of reflection. The projection is to the opposite side of the normal at the same angle as the incident wave.
Think of the wall as a mirror. The angle with which the wave impacts a mirror will be equal to the angle with which it is reflected, but mirrored across the normal.
← Didn't Know|Knew It →
Glass has an index of refraction of roughly 
. How much time would it take for light to pass through this glass if it were 
thick?
Glass has an index of refraction of roughly
Tap to reveal answer
Since the index of refraction is 1.5, we can determine the speed of light in the glass using the following equation:
Rearranged to solve for velocity:
Once the speed of light in the glass is known, we can use this quantity to determine how long it will take for the light to travel the width of the glass 
.
Since the index of refraction is 1.5, we can determine the speed of light in the glass using the following equation:
Rearranged to solve for velocity:
Once the speed of light in the glass is known, we can use this quantity to determine how long it will take for the light to travel the width of the glass
← Didn't Know|Knew It →
The refractive index of medium A is 1.2, while that of medium B is 1.36. Through which medium does light travel faster and at what speed does it travel?
The speed of light is 
.
The refractive index of medium A is 1.2, while that of medium B is 1.36. Through which medium does light travel faster and at what speed does it travel?
The speed of light is
Tap to reveal answer
The refractive index of a medium (n) is equal to the speed of light (c) divided by the velocity of light through the medium (v).
Rearranging the equation allows us to see the relationship regarding v.
The lower the refractive index, the faster the velocity of light. Medium A has the smaller refractive index. Light will travel faster through medium A at a velocity equal to the speed of light divided by the refractive index.
The refractive index of a medium (n) is equal to the speed of light (c) divided by the velocity of light through the medium (v).
Rearranging the equation allows us to see the relationship regarding v.
The lower the refractive index, the faster the velocity of light. Medium A has the smaller refractive index. Light will travel faster through medium A at a velocity equal to the speed of light divided by the refractive index.
← Didn't Know|Knew It →
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
The velocity of the light when it moves from air to glass.
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
The velocity of the light when it moves from air to glass.
Tap to reveal answer
This question asks us to consider the relationship between velocity and index of refraction of a medium. If we think back to the definition of index of refraction, we know that it is defined by the ratio of the velocity of light in a vacuum and the velocity of light in some other medium.
n is the index of refraction, c is the speed of light in a vacuum, and v is the speed of light in the new medium.
We can see that n and v are inversely proportional, meaning that the higher the n, the lower the velocity. As the light moved from air (n =1) to glass (n = 1.5), the n increased, and thus the velocity must decrease because the speed of light in a vacuum is constant.
This question asks us to consider the relationship between velocity and index of refraction of a medium. If we think back to the definition of index of refraction, we know that it is defined by the ratio of the velocity of light in a vacuum and the velocity of light in some other medium.
n is the index of refraction, c is the speed of light in a vacuum, and v is the speed of light in the new medium.
We can see that n and v are inversely proportional, meaning that the higher the n, the lower the velocity. As the light moved from air (n =1) to glass (n = 1.5), the n increased, and thus the velocity must decrease because the speed of light in a vacuum is constant.
← Didn't Know|Knew It →
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
As light exits from the wall of the cuvette into the solution, its wavelength .
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
As light exits from the wall of the cuvette into the solution, its wavelength .
Tap to reveal answer
This question asks us to find the relationship between the wavelength and index of refraction. We will need to know two equations to compute the relationship between the two.
First, we need to relate velocity and index of refraction. The definition of index of refraction allows us to relate the two.
We also know the relationship between velocity and wavelength.
We can now set these formulas equal to each other to find the relationship between wavelength and index of refraction.
We can see that 
and n are inversely related. If n decreases, the wavelength must increase. In our problem, light in moving from a higher index of refraction to a lower one, meaning the wavelength gets longer (increases).
This question asks us to find the relationship between the wavelength and index of refraction. We will need to know two equations to compute the relationship between the two.
First, we need to relate velocity and index of refraction. The definition of index of refraction allows us to relate the two.
We also know the relationship between velocity and wavelength.
We can now set these formulas equal to each other to find the relationship between wavelength and index of refraction.
We can see that
← Didn't Know|Knew It →
How long will it take a photon to travel 
through mineral oil?
How long will it take a photon to travel
Tap to reveal answer
The index of refraction is equal to the speed of light in a medium divided by the speed of light in a vacuum.
We can find the time to travel a given distance by manipulating this equation and combining it with the equation for rate: 
.
Plug in the given values and solve for the velocity in the medium.
Now we can return to the rate equation and solve for the time to travel 
.
We can recognize that the answer can be simplified by converting to nanoseconds.
The index of refraction is equal to the speed of light in a medium divided by the speed of light in a vacuum.
We can find the time to travel a given distance by manipulating this equation and combining it with the equation for rate:
Plug in the given values and solve for the velocity in the medium.
Now we can return to the rate equation and solve for the time to travel
We can recognize that the answer can be simplified by converting to nanoseconds.
← Didn't Know|Knew It →
Which of the following does not take place when a light wave travels from a medium with a high index of refraction into one with a lower index of refraction?
Which of the following does not take place when a light wave travels from a medium with a high index of refraction into one with a lower index of refraction?
Tap to reveal answer
As the wave travels into the less dense medium, it speeds up, bending away from the normal line. The index of refraction tells the ratio of the velocity in a vacuum in relation to the velocity the medium; thus, the velocity will be greater in a medium with a lower index of refraction.
Frequency remains the same regardless of medium, however, since the velocity changes, the wavelength must accommodate this change.
If velocity increases and frequency remains constant, wavelength must also increase.
Finally, a phase shift only occurs when a light ray reflects from the surface of a more dense medium.
As the wave travels into the less dense medium, it speeds up, bending away from the normal line. The index of refraction tells the ratio of the velocity in a vacuum in relation to the velocity the medium; thus, the velocity will be greater in a medium with a lower index of refraction.
Frequency remains the same regardless of medium, however, since the velocity changes, the wavelength must accommodate this change.
If velocity increases and frequency remains constant, wavelength must also increase.
Finally, a phase shift only occurs when a light ray reflects from the surface of a more dense medium.
← Didn't Know|Knew It →
What is the index of refraction for a material in which light travels at 
?
What is the index of refraction for a material in which light travels at
Tap to reveal answer
Relevant equations:
To find index of refraction, divide the speed of light in a vacuum by the speed of light in the material:
Relevant equations:
To find index of refraction, divide the speed of light in a vacuum by the speed of light in the material:
← Didn't Know|Knew It →
The refractive index of medium A is 1.2, while that of medium B is 1.36. Through which medium does light travel faster and at what speed does it travel?
The speed of light is .
The refractive index of medium A is 1.2, while that of medium B is 1.36. Through which medium does light travel faster and at what speed does it travel?
The speed of light is
Tap to reveal answer
The refractive index of a medium (n) is equal to the speed of light (c) divided by the velocity of light through the medium (v).
Rearranging the equation allows us to see the relationship regarding v.
The lower the refractive index, the faster the velocity of light. Medium A has the smaller refractive index. Light will travel faster through medium A at a velocity equal to the speed of light divided by the refractive index.
The refractive index of a medium (n) is equal to the speed of light (c) divided by the velocity of light through the medium (v).
Rearranging the equation allows us to see the relationship regarding v.
The lower the refractive index, the faster the velocity of light. Medium A has the smaller refractive index. Light will travel faster through medium A at a velocity equal to the speed of light divided by the refractive index.
← Didn't Know|Knew It →
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
The velocity of the light when it moves from air to glass.
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
The velocity of the light when it moves from air to glass.
Tap to reveal answer
This question asks us to consider the relationship between velocity and index of refraction of a medium. If we think back to the definition of index of refraction, we know that it is defined by the ratio of the velocity of light in a vacuum and the velocity of light in some other medium.
n is the index of refraction, c is the speed of light in a vacuum, and v is the speed of light in the new medium.
We can see that n and v are inversely proportional, meaning that the higher the n, the lower the velocity. As the light moved from air (n =1) to glass (n = 1.5), the n increased, and thus the velocity must decrease because the speed of light in a vacuum is constant.
This question asks us to consider the relationship between velocity and index of refraction of a medium. If we think back to the definition of index of refraction, we know that it is defined by the ratio of the velocity of light in a vacuum and the velocity of light in some other medium.
n is the index of refraction, c is the speed of light in a vacuum, and v is the speed of light in the new medium.
We can see that n and v are inversely proportional, meaning that the higher the n, the lower the velocity. As the light moved from air (n =1) to glass (n = 1.5), the n increased, and thus the velocity must decrease because the speed of light in a vacuum is constant.
← Didn't Know|Knew It →
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
As light exits from the wall of the cuvette into the solution, its wavelength .
An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.
As light exits from the wall of the cuvette into the solution, its wavelength .
Tap to reveal answer
This question asks us to find the relationship between the wavelength and index of refraction. We will need to know two equations to compute the relationship between the two.
First, we need to relate velocity and index of refraction. The definition of index of refraction allows us to relate the two.
We also know the relationship between velocity and wavelength.
We can now set these formulas equal to each other to find the relationship between wavelength and index of refraction.
We can see that and n are inversely related. If n decreases, the wavelength must increase. In our problem, light in moving from a higher index of refraction to a lower one, meaning the wavelength gets longer (increases).
This question asks us to find the relationship between the wavelength and index of refraction. We will need to know two equations to compute the relationship between the two.
First, we need to relate velocity and index of refraction. The definition of index of refraction allows us to relate the two.
We also know the relationship between velocity and wavelength.
We can now set these formulas equal to each other to find the relationship between wavelength and index of refraction.
We can see that
← Didn't Know|Knew It →
How long will it take a photon to travel through mineral oil?
How long will it take a photon to travel
Tap to reveal answer
The index of refraction is equal to the speed of light in a medium divided by the speed of light in a vacuum.
We can find the time to travel a given distance by manipulating this equation and combining it with the equation for rate: .
Plug in the given values and solve for the velocity in the medium.
Now we can return to the rate equation and solve for the time to travel .
We can recognize that the answer can be simplified by converting to nanoseconds.
The index of refraction is equal to the speed of light in a medium divided by the speed of light in a vacuum.
We can find the time to travel a given distance by manipulating this equation and combining it with the equation for rate:
Plug in the given values and solve for the velocity in the medium.
Now we can return to the rate equation and solve for the time to travel
We can recognize that the answer can be simplified by converting to nanoseconds.
← Didn't Know|Knew It →
Which of the following does not take place when a light wave travels from a medium with a high index of refraction into one with a lower index of refraction?
Which of the following does not take place when a light wave travels from a medium with a high index of refraction into one with a lower index of refraction?
Tap to reveal answer
As the wave travels into the less dense medium, it speeds up, bending away from the normal line. The index of refraction tells the ratio of the velocity in a vacuum in relation to the velocity the medium; thus, the velocity will be greater in a medium with a lower index of refraction.
Frequency remains the same regardless of medium, however, since the velocity changes, the wavelength must accommodate this change.
If velocity increases and frequency remains constant, wavelength must also increase.
Finally, a phase shift only occurs when a light ray reflects from the surface of a more dense medium.
As the wave travels into the less dense medium, it speeds up, bending away from the normal line. The index of refraction tells the ratio of the velocity in a vacuum in relation to the velocity the medium; thus, the velocity will be greater in a medium with a lower index of refraction.
Frequency remains the same regardless of medium, however, since the velocity changes, the wavelength must accommodate this change.
If velocity increases and frequency remains constant, wavelength must also increase.
Finally, a phase shift only occurs when a light ray reflects from the surface of a more dense medium.
← Didn't Know|Knew It →
What is the index of refraction for a material in which light travels at ?
What is the index of refraction for a material in which light travels at
Tap to reveal answer
Relevant equations:
To find index of refraction, divide the speed of light in a vacuum by the speed of light in the material:
Relevant equations:
To find index of refraction, divide the speed of light in a vacuum by the speed of light in the material:
← Didn't Know|Knew It →
A scuba diver wearing a head lamp is returning to the surface of the Pacific Ocean. What is the index of refraction of the ocean water if the smallest angle resulting in total internal reflection is 35 degrees from the vertical?
A scuba diver wearing a head lamp is returning to the surface of the Pacific Ocean. What is the index of refraction of the ocean water if the smallest angle resulting in total internal reflection is 35 degrees from the vertical?
Tap to reveal answer
We can use Snell's law to calculate the index of refraction of the water:
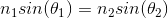
Where the subscript 1 denotes water and subscript 2 denotes air.
At the first incidence of total internal reflection, the angle of refraction is 90 degrees. Therefore, the sine function becomes 1, giving us the formula:
Rearranging for the index of water:
We can use Snell's law to calculate the index of refraction of the water:
Where the subscript 1 denotes water and subscript 2 denotes air.
At the first incidence of total internal reflection, the angle of refraction is 90 degrees. Therefore, the sine function becomes 1, giving us the formula:
Rearranging for the index of water:
← Didn't Know|Knew It →
In a microscope has a 
tube length and objective lens with a focal length of 
. The viewer's eye is 
from the objective lens, and they desire a magnification of 
. What must the focal length of the eyepiece lens be to achieve this magnification?
In a microscope has a
Tap to reveal answer
The total magnification of a compound microscope is the product of the objective lens magnification and the eyepiece magnification.
Objective magnification and eyepiece magnification are given by the following equations:
We are given the tube length and focal length of the objective lens, allowing us to solve for its magnification.
We also know the distance of the viewer's eye. Use this value in the eyepiece magnification equation.
Finally, combine the eyepiece magnification and objective lens magnification into the original equation for total magnification.
Use the given value for total magnification to solve for the focal length of the eyepiece lens.
The total magnification of a compound microscope is the product of the objective lens magnification and the eyepiece magnification.
Objective magnification and eyepiece magnification are given by the following equations:
We are given the tube length and focal length of the objective lens, allowing us to solve for its magnification.
We also know the distance of the viewer's eye. Use this value in the eyepiece magnification equation.
Finally, combine the eyepiece magnification and objective lens magnification into the original equation for total magnification.
Use the given value for total magnification to solve for the focal length of the eyepiece lens.
← Didn't Know|Knew It →
A compound microscope consists of an eyepiece with an angular magnification of 25 and an objective lens of unknown focal length. If the length of the microscope tube is 25cm, what magnitude of objective focal length is necessary to achieve an overall magnification of 500?
A compound microscope consists of an eyepiece with an angular magnification of 25 and an objective lens of unknown focal length. If the length of the microscope tube is 25cm, what magnitude of objective focal length is necessary to achieve an overall magnification of 500?
Tap to reveal answer
Relevant equations:
= length of microscope tube
= focal length of objective
= focal length of eyepiece
= linear magnification of objective
= angular magnification of eyepiece
= total magnification of microscope
Given:
Step 1: Plug the expression for 
into the equation for total magnification, 
.
Step 2: Rearrange to isolate the unknown, 
Step 3: Plug in given quantities, taking the absolute value to find the magnitude of 
.
Relevant equations:
Given:
Step 1: Plug the expression for
Step 2: Rearrange to isolate the unknown,
Step 3: Plug in given quantities, taking the absolute value to find the magnitude of
← Didn't Know|Knew It →
What diameter of telescope objective lens is necessary to resolve two stars that primarily emit 600nm light and have an angular separation of 
?
What diameter of telescope objective lens is necessary to resolve two stars that primarily emit 600nm light and have an angular separation of
Tap to reveal answer
Relevant equations:
= angular separation of sources, in radians
= wavelength of light emitted by sources, in meters
= diameter of telescope
Step 1: Rearrange equation to isolate the unknown, 
:
Step 2: Plug in the given numbers for wavelength and angular separation:
Relevant equations:
Step 1: Rearrange equation to isolate the unknown,
Step 2: Plug in the given numbers for wavelength and angular separation:
← Didn't Know|Knew It →