General Chemistry - MCAT Chemical and Physical Foundations of Biological Systems
Card 1 of 3171
A solution of acetic acid (pKa = 4.75) has a pH of 6.75. The ratio of acid to conjugate base is .
A solution of acetic acid (pKa = 4.75) has a pH of 6.75. The ratio of acid to conjugate base is .
Tap to reveal answer
Use the Henderson-Hasselbalch equation: ![\dpi{100} \small $pH=pK_{a}$+log\left $\frac{\left[ $A^{-}$$ \right]}{\left[ HA \right]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/18757/gif.latex)
![\dpi{100} \small 6.75=4.75+log\left $\frac{\left [ $A^{-}$$ \right ]}{\left [ HA \right ]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/18758/gif.latex)
![\dpi{100} \small 2=log\left $\frac{\left[ $A^{-}$$ \right]}{\left[ HA \right]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/18759/gif.latex)
![\dpi{100} \small $10^{2}$=\left $\frac{\left [ $A^{-}$$ \right ]}{\left [ HA \right ]}=100](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/18760/gif.latex)
We want the ratio of acid to conjugate base, which would be the reciprocal, ![\dpi{100} \small $10^{2}$=\left $\frac{\left[ HA \right]}{\left[ $A^{-}$$ \right]}=\frac{1}{100}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/18761/gif.latex)
Use the Henderson-Hasselbalch equation:
We want the ratio of acid to conjugate base, which would be the reciprocal,
← Didn't Know|Knew It →
You need to produce a buffer with pH of  . You have a solution with
. You have a solution with  of acetic acid (
of acetic acid ( ). How many moles of sodium acetate must you add to achieve the desired pH?
). How many moles of sodium acetate must you add to achieve the desired pH?
You need to produce a buffer with pH of 


Tap to reveal answer
Use the Henderson-Hasselbalch equation: ![\dpi{100} \small $pH=pK_{a}$+log\left $\frac{\left[ $A^{-}$$ \right]}{\left[ HA \right]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/18762/gif.latex)
Assuming that these ions occupy the same volume, ![\dpi{100} \small log=\frac{\left[ $A^{-}$$ \right]}{\left[ HA \right]}=log$\frac{\left ( mol\ of\ $A^{-}$$\right )}{\left ( mol\ of\ HA\right )}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/18763/gif.latex)
We know we have 30g of acetic acid, which is equal to 0.5mol (you should memorize the formula for acetic acid).
Plugging in our values gives us $5.75=4.75+log$\frac{A^{-}$$}{0.5}
Solving for A– gives us 5mol.
Use the Henderson-Hasselbalch equation:
Assuming that these ions occupy the same volume,
We know we have 30g of acetic acid, which is equal to 0.5mol (you should memorize the formula for acetic acid).
Plugging in our values gives us $5.75=4.75+log$\frac{A^{-}$$}{0.5}
Solving for A– gives us 5mol.
← Didn't Know|Knew It →
NaOH is added to a 500mL of 2M acetic acid. If the pKa value of acetic acid is approximately 4.8, what volume of 2M NaOH must be added so that the pH of the solution is 4.8?
NaOH is added to a 500mL of 2M acetic acid. If the pKa value of acetic acid is approximately 4.8, what volume of 2M NaOH must be added so that the pH of the solution is 4.8?
Tap to reveal answer
To solve this question you need to think about the chemical reaction occurring.

We can ignore water and sodium ions for the sake of this question. The reactants exist in a 1:1 ratio, so that for every mol of NaOH we add, we lose one mol of acetic acid and gain one mol of acetate. We can determine the moles of acetic acid by using M = mol/L, which gives us mol = ML = (2M) * (0.5L) = 1mol acetic acid. If we use the Hendersen Hasselbach equation we can see that the pH equals the pKa when the concentration of conjugate base (acetate) equals the concentration of acid.
![pH=pK_a+log$\frac{[base]}{[acid]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26258/gif.latex)
If we have 1mol of acetic acid and add 0.5mol of NaOH, we will lose 0.5mol of acetic acid and gain 0.5mol of acetate. We will then be at a point where acetic acid equals acetate. This is summarized in the ICE table below. Now we know the moles of NaOH (0.5 moles) and the concentration (2M) so we can find the volume by doing M = mol/L.
L = mol/M = (0.5mol)/(2M) = 0.25L
| | Acetic acid | NaOH | Acetate | |
| -------------- | --------- | --------- | -------- |
| I | 1 mol | 0.5 mol | 0 mol |
| C | -0.5 mol | -0.5 mol | +0.5 mol |
| E | 0.5 mol | 0 mol | 0.5 mol |
To solve this question you need to think about the chemical reaction occurring.
We can ignore water and sodium ions for the sake of this question. The reactants exist in a 1:1 ratio, so that for every mol of NaOH we add, we lose one mol of acetic acid and gain one mol of acetate. We can determine the moles of acetic acid by using M = mol/L, which gives us mol = ML = (2M) * (0.5L) = 1mol acetic acid. If we use the Hendersen Hasselbach equation we can see that the pH equals the pKa when the concentration of conjugate base (acetate) equals the concentration of acid.
If we have 1mol of acetic acid and add 0.5mol of NaOH, we will lose 0.5mol of acetic acid and gain 0.5mol of acetate. We will then be at a point where acetic acid equals acetate. This is summarized in the ICE table below. Now we know the moles of NaOH (0.5 moles) and the concentration (2M) so we can find the volume by doing M = mol/L.
L = mol/M = (0.5mol)/(2M) = 0.25L
| | Acetic acid | NaOH | Acetate | | | -------------- | --------- | --------- | -------- | | I | 1 mol | 0.5 mol | 0 mol | | C | -0.5 mol | -0.5 mol | +0.5 mol | | E | 0.5 mol | 0 mol | 0.5 mol |
← Didn't Know|Knew It →
The Ka for HCN is  .
.
If there is a solution of 2M HCN, what concentration of NaCN is needed in order for the pH to be 9.2?
The Ka for HCN is 
If there is a solution of 2M HCN, what concentration of NaCN is needed in order for the pH to be 9.2?
Tap to reveal answer
To answer this question, we need to be able to compare the concentrations of acid and conjugate base in the solution with the pH. The Henderson-Hasselbach equation is used to compare these values, and is written as:![\small pH = pK_{a} + log\frac{[A^{-}]}{[HA]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86323/gif.latex) . In this question, this equation can be written with the given values of Ka and pH.
. In this question, this equation can be written with the given values of Ka and pH.
![9.2=-log(6.2*10^{-10})+log\frac{[CN^-]}{[HCN]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/123432/gif.latex)
Since we know the Ka of HCN, we can derive the pKa, which turns out to be 9.2.
![pH=9.2+log\frac{[CN^-]}{[HCN]}=9.2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86324/gif.latex)
As a result, we want to see to it that the amount of conjugate base is equal to the concentration of acid, so that ![\small log\frac{[A^{-}]}{[HA]} =0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/123433/gif.latex) . Because log(1) = 0, we want to see to it that the concentrations of the acid and the conjugate base are equal to one another. We know from the question that \[HCN\] = 2M.
. Because log(1) = 0, we want to see to it that the concentrations of the acid and the conjugate base are equal to one another. We know from the question that \[HCN\] = 2M.
![pH=9.2+log\frac{[CN^-]}{[2]}=9.2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86325/gif.latex)
![\frac{[CN^-]}{[2]}=1](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/123434/gif.latex)
![[CN^-]=2M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86326/gif.latex)
As a result, a concentration of 2M NaCN will allow the pH of the solution to be 9.2.
To answer this question, we need to be able to compare the concentrations of acid and conjugate base in the solution with the pH. The Henderson-Hasselbach equation is used to compare these values, and is written as:![\small pH = pK_{a} + log\frac{[A^{-}]}{[HA]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86323/gif.latex)
Since we know the Ka of HCN, we can derive the pKa, which turns out to be 9.2.
As a result, we want to see to it that the amount of conjugate base is equal to the concentration of acid, so that ![\small log\frac{[A^{-}]}{[HA]} =0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/123433/gif.latex)
As a result, a concentration of 2M NaCN will allow the pH of the solution to be 9.2.
← Didn't Know|Knew It →
A solution of hydrofluoric acid has a concentration of  .
.
The  for
for  is
is  .
.
If sodium hydroxide is slowly added to this solution, what will the pH be at the half equivalence point?
A solution of hydrofluoric acid has a concentration of 
The 


If sodium hydroxide is slowly added to this solution, what will the pH be at the half equivalence point?
Tap to reveal answer
If we use the Henderson-Hasselbalch equation, we do not need to worry about using the molar amounts of both the acid and the base. At the half equivalence point, the conjugate base concentration is equal to that of the weak acid. This means that the equation can be simplified.
Henderson-Hasselbalch equation:
![pH = $pK_{a}$ + $log$\frac{[A^{-}$$]}{[HA]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/299991/gif.latex)
Simplified equation for half equivalence point:

Because we know the acid dissociation constant for hydrofluoric acid, the pH is calculated as:
![pH = $-log[7.2*10^{-4}$] = 3.14](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/291161/gif.latex)
If we use the Henderson-Hasselbalch equation, we do not need to worry about using the molar amounts of both the acid and the base. At the half equivalence point, the conjugate base concentration is equal to that of the weak acid. This means that the equation can be simplified.
Henderson-Hasselbalch equation:
Simplified equation for half equivalence point:
Because we know the acid dissociation constant for hydrofluoric acid, the pH is calculated as:
← Didn't Know|Knew It →
Calculate the concentration of hydrogen ions in the following acetic acid solution.

![$\frac{[CH_3COOH]}{[CH_3COO^-]}$ = 0.5](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320078/gif.latex)
Calculate the concentration of hydrogen ions in the following acetic acid solution.
Tap to reveal answer
To answer this question you need to use the Henderson-Hasselbalch equation:
![pH = pKa +log$\frac{[conjugate: base]}{[acid]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320079/gif.latex)
The ratio given in the question is ![$\frac{[CH_3COOH]}{[CH_3COO^-]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320080/gif.latex) , or
, or ![$\frac{[acid]}{[conjugate : base]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320081/gif.latex) .
.
To use the correct ratio for the Henderson-Hasselbalch equation, we need to convert this ratio to its reciprocal:

Plugging the given values into the equation gives us:

The question is asking for the concentration of hydrogen ions. To solve for this we have to use the definition of pH.
![pH = -log[H^+]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320084/gif.latex)
Solving for the concentration of hydrogen ions gives us:
![[H+] = 10^$-^p$^H](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320085/gif.latex)
![[H^+] = 10^$-^5$^$.^0$^6](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320086/gif.latex)
![[H+] = 8.69 * 10^$-^6M$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/336944/gif.latex)
To answer this question you need to use the Henderson-Hasselbalch equation:
The ratio given in the question is ![$\frac{[CH_3COOH]}{[CH_3COO^-]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320080/gif.latex)
![$\frac{[acid]}{[conjugate : base]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320081/gif.latex)
To use the correct ratio for the Henderson-Hasselbalch equation, we need to convert this ratio to its reciprocal:
Plugging the given values into the equation gives us:
The question is asking for the concentration of hydrogen ions. To solve for this we have to use the definition of pH.
Solving for the concentration of hydrogen ions gives us:
← Didn't Know|Knew It →
Which of the following is true regarding the Henderson-Hasselbalch equation?
I. The pH of the solution is always greater than the pKa of the solution
II. As the ratio of conjugate base to acid increases, the pH increases
III. The hydrogen ion concentration can never equal the acid dissociation constant
Which of the following is true regarding the Henderson-Hasselbalch equation?
I. The pH of the solution is always greater than the pKa of the solution
II. As the ratio of conjugate base to acid increases, the pH increases
III. The hydrogen ion concentration can never equal the acid dissociation constant
Tap to reveal answer
The Henderson-Hasselbalch equation is a tool that allows us to calculate the pH of an acid solution using the pKa of the acid and the relative concentrations of the acid and its conjugate base. It is defined as:
![pH = pKa + log$\frac{[A-]}{[HA]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320068/gif.latex)
By looking at the equation we can determine that if the ratio inside the logarithm is greater than 1, then the pH of the solution will be greater than the pKa; however, if the ratio is less than 1 (meaning, if the concentration of the acid is greater than the concentration of conjugate base), then the pH will be less than the pKa. Statement I is false.
Increasing the ratio of ![[A^-]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320073/gif.latex) to
to ![[HA]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320074/gif.latex) will increase the logarithm, and subsequently the pH of the solution. This makes sense because you will have more conjugate base than acid, thereby making the solution more alkaline and increasing the pH. Statement II is true.
will increase the logarithm, and subsequently the pH of the solution. This makes sense because you will have more conjugate base than acid, thereby making the solution more alkaline and increasing the pH. Statement II is true.
pH and pKa are defined as follows:
![pH = -log[H^+]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320075/gif.latex)

If we have the same concentration of hydrogen ions as the acid dissociation constant ( ), then the pH will equal the pKa. According to the Henderson-Hasselbalch equation, the pH equals the pKa if the concentration of the conjugate base equals the concentration of acid; therefore, it is possible for the hydrogen ion concentration to equal the acid dissociation constant. Statement III is false.
), then the pH will equal the pKa. According to the Henderson-Hasselbalch equation, the pH equals the pKa if the concentration of the conjugate base equals the concentration of acid; therefore, it is possible for the hydrogen ion concentration to equal the acid dissociation constant. Statement III is false.
The Henderson-Hasselbalch equation is a tool that allows us to calculate the pH of an acid solution using the pKa of the acid and the relative concentrations of the acid and its conjugate base. It is defined as:
By looking at the equation we can determine that if the ratio inside the logarithm is greater than 1, then the pH of the solution will be greater than the pKa; however, if the ratio is less than 1 (meaning, if the concentration of the acid is greater than the concentration of conjugate base), then the pH will be less than the pKa. Statement I is false.
Increasing the ratio of ![[A^-]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320073/gif.latex)
![[HA]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320074/gif.latex)
pH and pKa are defined as follows:
If we have the same concentration of hydrogen ions as the acid dissociation constant (
← Didn't Know|Knew It →
Increasing the volume of an acid solution the pH of the solution and the pKa of the acid.
Increasing the volume of an acid solution the pH of the solution and the pKa of the acid.
Tap to reveal answer
The definition of pH is as follows:
![pH = -log[H^+]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320088/gif.latex)
The pH of a solution heavily depends on the concentration of hydrogen ions. Recall that the concentration is in molarity (M), which is defined as:

Increasing the volume of the solution will decrease the concentration (molarity) of the hydrogen ions which will, subsequently, increase the pH; therefore, increasing volume will increase the pH.
Recall that pKa of an acid can never be altered. pKa is a reflection of the strength of the acid, which stays constant under all circumstances.
The definition of pH is as follows:
The pH of a solution heavily depends on the concentration of hydrogen ions. Recall that the concentration is in molarity (M), which is defined as:
Increasing the volume of the solution will decrease the concentration (molarity) of the hydrogen ions which will, subsequently, increase the pH; therefore, increasing volume will increase the pH.
Recall that pKa of an acid can never be altered. pKa is a reflection of the strength of the acid, which stays constant under all circumstances.
← Didn't Know|Knew It →
A researcher prepares two solutions. Solution A contains an unknown acid, HA, and solution B contains an unknown acid, HB. The researcher performs several tests and collects the following data.
1. Both solutions contain weak acids
2. ![$\frac{[A^-]}{[HA]}$ = 1000](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320096/gif.latex)
3. 
4. ![$\frac{[B^-]}{[HB]}$ = 100](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320098/gif.latex)
5. 
What can you conclude about these two solutions?
A researcher prepares two solutions. Solution A contains an unknown acid, HA, and solution B contains an unknown acid, HB. The researcher performs several tests and collects the following data.
1. Both solutions contain weak acids
2.
3.
4.
5.
What can you conclude about these two solutions?
Tap to reveal answer
The Henderson-Hasselbalch equation states that:
![pH = pKa + log$\frac{[A^-]}{[HA]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320100/gif.latex)
The question gives us information regarding the ratio of conjugate base to acid AND the pH for each acidic solution. Using this information, we can solve for the pKa values of both solutions.
![pKa = pH - log$\frac{[A^-]}{[HA]}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/320103/gif.latex)


The pKa values of both solutions are the same. This means that both solution contains the same acid; therefore, the identity of HA is the same as the identity of HB.
The hydrogen ion concentration of solution A is lower than that of solution B because the pH of solution A is greater. Acidity, or strength, of an acid is determined by the pKa. Since we have the same pKa for both acids, HA and HB will have the same acidity. Acid dissociation constant, Ka, is defined as:

Acid dissociation constant only depends on the pKa; therefore, the Ka for both acids is the same.
The Henderson-Hasselbalch equation states that:
The question gives us information regarding the ratio of conjugate base to acid AND the pH for each acidic solution. Using this information, we can solve for the pKa values of both solutions.
The pKa values of both solutions are the same. This means that both solution contains the same acid; therefore, the identity of HA is the same as the identity of HB.
The hydrogen ion concentration of solution A is lower than that of solution B because the pH of solution A is greater. Acidity, or strength, of an acid is determined by the pKa. Since we have the same pKa for both acids, HA and HB will have the same acidity. Acid dissociation constant, Ka, is defined as:
Acid dissociation constant only depends on the pKa; therefore, the Ka for both acids is the same.
← Didn't Know|Knew It →
Consider the half reaction below.
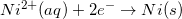

Which of the following statements is true about the oxidation of nickel?
Consider the half reaction below.
Which of the following statements is true about the oxidation of nickel?
Tap to reveal answer
Reduction potentials are typically provided in table form. Since the oxidation potential of an element is the negative of the reduction potential, it can be determined by viewing a reduction table.
Since the reduction potential for nickel is given as –0.23V, we can conclude that the oxidation potential for nickel is 0.23V.
Reduction potentials are typically provided in table form. Since the oxidation potential of an element is the negative of the reduction potential, it can be determined by viewing a reduction table.
Since the reduction potential for nickel is given as –0.23V, we can conclude that the oxidation potential for nickel is 0.23V.
← Didn't Know|Knew It →
The standard reduction potentials for iron and nickel are as follows:




If a galvanic cell is made using these two metals, what is the standard voltage for the cell?
The standard reduction potentials for iron and nickel are as follows:


If a galvanic cell is made using these two metals, what is the standard voltage for the cell?
Tap to reveal answer
A galvanic cell is spontaneous, meaning that there will be a positive cell voltage. In order for this to take place, the more negative reduction potential must be flipped so that the metal is oxidized.




Adding these values together gives a standard cell voltage of  .
.
A galvanic cell is spontaneous, meaning that there will be a positive cell voltage. In order for this to take place, the more negative reduction potential must be flipped so that the metal is oxidized.


Adding these values together gives a standard cell voltage of 
← Didn't Know|Knew It →
What is the electron configuration of potassium after it obtains a +1 charge?
What is the electron configuration of potassium after it obtains a +1 charge?
Tap to reveal answer
Potassium (K) is orignially in the electron configuration of \[Ar\]4s1. To obtain a +1 charge it loses an electron, resulting in a configuration of \[Ar\].
Potassium (K) is orignially in the electron configuration of \[Ar\]4s1. To obtain a +1 charge it loses an electron, resulting in a configuration of \[Ar\].
← Didn't Know|Knew It →
What is the electron configuration of Fe+?
What is the electron configuration of Fe+?
Tap to reveal answer
When an element loses an electron it is generally taken away from the highest electron shell. The electron configuration of iron (Fe) is  . The 4s orbital is farther away from the nucleus than the 3d orbital, therefore the electron configuration of Fe+ will be
. The 4s orbital is farther away from the nucleus than the 3d orbital, therefore the electron configuration of Fe+ will be  .
.
When an element loses an electron it is generally taken away from the highest electron shell. The electron configuration of iron (Fe) is 

← Didn't Know|Knew It →
An atom with the electron configuration 1s22s22p6 could be any of the following except .
An atom with the electron configuration 1s22s22p6 could be any of the following except .
Tap to reveal answer
This particular configuration denotes a particle with ten total electrons. The sodium atom, with eleven electrons, is the only one listed that could not have this configuration. Ionized sodium, however, symbolized as Na+, does apply. (Be careful to distinguish neutral atoms and ions).
This particular configuration denotes a particle with ten total electrons. The sodium atom, with eleven electrons, is the only one listed that could not have this configuration. Ionized sodium, however, symbolized as Na+, does apply. (Be careful to distinguish neutral atoms and ions).
← Didn't Know|Knew It →
Which of the following is the correct electronic configuration for vanadium?
Which of the following is the correct electronic configuration for vanadium?
Tap to reveal answer
When determining electronic configuration, the answer is made much easier by starting with the next smallest noble gas in brackets. As a result, \[Ar\] is an appropriate way to incorporate every previous electron before argon.
After argon, vanadium has five other electrons to distribute, and because vanadium is a transitional element, it will fill its 3d subshells before filling the 4p subshells. The 4s subshell is filled first, and the last three electrons are placed into the 3d subshells.
\[Ar\]3d34s2
When determining electronic configuration, the answer is made much easier by starting with the next smallest noble gas in brackets. As a result, \[Ar\] is an appropriate way to incorporate every previous electron before argon.
After argon, vanadium has five other electrons to distribute, and because vanadium is a transitional element, it will fill its 3d subshells before filling the 4p subshells. The 4s subshell is filled first, and the last three electrons are placed into the 3d subshells.
\[Ar\]3d34s2
← Didn't Know|Knew It →
What is the correct electronic structure for  ?
?
What is the correct electronic structure for 
Tap to reveal answer
Were this question asking for the electronic structure of magnesium (Mg) in its ground state,  would be the correct answer; however, the
would be the correct answer; however, the  charge on
charge on  means that the molecule shed two valence electrons to achieve a more stable orbital. Those electrons will be shed from the outermost valence shell, which in this case is the
means that the molecule shed two valence electrons to achieve a more stable orbital. Those electrons will be shed from the outermost valence shell, which in this case is the  shell; therefore,
shell; therefore,  is correct.
is correct.
Note that the ground state of magnesium will have twelve electrons (the same as its atomic number), while the ion will have ten.
Were this question asking for the electronic structure of magnesium (Mg) in its ground state, 




Note that the ground state of magnesium will have twelve electrons (the same as its atomic number), while the ion will have ten.
← Didn't Know|Knew It →
An electron in which of the following orbitals is closest to the nucleus?
An electron in which of the following orbitals is closest to the nucleus?
Tap to reveal answer
Nuclear orbitals will always fill from the innermost to the outermost subshells. Using the  rule, we can approximate the order in which these orbitals will fill. Because electrons fill starting with the centermost orbitals, the electron that is closest to the nucleus will belong to the orbital that fills first.
rule, we can approximate the order in which these orbitals will fill. Because electrons fill starting with the centermost orbitals, the electron that is closest to the nucleus will belong to the orbital that fills first.
 corresponds to the principle quantum number, the first number in the given orbital location.
corresponds to the principle quantum number, the first number in the given orbital location.  is the azimuthal quantum number, and dictates the shape of the orbital.
is the azimuthal quantum number, and dictates the shape of the orbital.




5s and 3d produce the same number from the  equation, but in the event of a tie we always pick the orbital with the lowest letter (s < p < d < f). The innermost orbital will be 5s.
equation, but in the event of a tie we always pick the orbital with the lowest letter (s < p < d < f). The innermost orbital will be 5s.




Nuclear orbitals will always fill from the innermost to the outermost subshells. Using the 





5s and 3d produce the same number from the 
← Didn't Know|Knew It →
Which of the following species is represented by the given electron configuration?

Which of the following species is represented by the given electron configuration?
Tap to reveal answer
Due to the phenomenon of half-orbital stability in the transition metals, electrons can easily move between 4s and 3d orbitals. The atom achieves greater stability from having only one atom in the 4s orbital, allowing a half-filled 3d orbital, as opposed to a full 4s orbital and four electrons in the 3d subshell.
For elements like chromium and copper, which could have valence shell configurations of 4s23d4 and _4s_23d9, respectively, an electron from the 4s orbital jumps down to the 3d orbital to harness added stability from the half-filled orbital. The given electron configuration is that of chromium.
Note that you can also solve this question by counting the electrons to determine the atomic number. In this case, the electrons add up to 24, indicating the twenty-fourth element: chromium.
Due to the phenomenon of half-orbital stability in the transition metals, electrons can easily move between 4s and 3d orbitals. The atom achieves greater stability from having only one atom in the 4s orbital, allowing a half-filled 3d orbital, as opposed to a full 4s orbital and four electrons in the 3d subshell.
For elements like chromium and copper, which could have valence shell configurations of 4s23d4 and _4s_23d9, respectively, an electron from the 4s orbital jumps down to the 3d orbital to harness added stability from the half-filled orbital. The given electron configuration is that of chromium.
Note that you can also solve this question by counting the electrons to determine the atomic number. In this case, the electrons add up to 24, indicating the twenty-fourth element: chromium.
← Didn't Know|Knew It →
Which element has the most valence electrons?
Which element has the most valence electrons?
Tap to reveal answer
Valence electrons will be housed in the outer shell (highest numbered orbital) of the electron configuration.
Calcium: 
Magnesium: ![[Ne]3s^ 2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/123245/gif.latex)
Zinc: 
Copper: 
Arsenic: 
Calcium, magnesium, and zinc all have two valence electrons in their highest energy orbital. Copper has only one valence electron. Arsenic has five total valence electrons in the fourth shell.
Valence electrons will be housed in the outer shell (highest numbered orbital) of the electron configuration.
Calcium:
Magnesium:
Zinc:
Copper:
Arsenic:
Calcium, magnesium, and zinc all have two valence electrons in their highest energy orbital. Copper has only one valence electron. Arsenic has five total valence electrons in the fourth shell.
← Didn't Know|Knew It →
What is the correct electron configuration of  ?
?
What is the correct electron configuration of 
Tap to reveal answer
An atom that has a charge of  has lost two electrons. The two lost are always the valence electrons, which are most easily taken from the molecule. Strontium has a normal electron configuration with 38 electrons. In shorthand notation, this would be:
has lost two electrons. The two lost are always the valence electrons, which are most easily taken from the molecule. Strontium has a normal electron configuration with 38 electrons. In shorthand notation, this would be:

Losing two valence electrons will remove the 5s electrons. This leave the configuration as:
![[Kr]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/132321/gif.latex)
This makes sense because krypton has a stable valence octet. Strontium is stable as an ion, meaning that it will also have an octet, allowing it to match the configuration for krypton.
An atom that has a charge of 
Losing two valence electrons will remove the 5s electrons. This leave the configuration as:
This makes sense because krypton has a stable valence octet. Strontium is stable as an ion, meaning that it will also have an octet, allowing it to match the configuration for krypton.
← Didn't Know|Knew It →