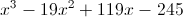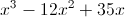Understanding Zeros of a Polynomial

Help Questions

Math › Understanding Zeros of a Polynomial

Questions 1 - 4

1

Factor the polynomial if the expression is equal to zero when $x=-6, -4,\ or\ 2$ .

Explanation

Knowing the zeroes makes it relatively easy to factor the polynomial.

The expression fits the description of the zeroes.

Now we need to check the answer.

$\small (x^2+2x-8)(x+6)=x^3+6x^2+2x^2+12x-8x-48=x^3+8x^2+4x-48$

We are able to get back to the original expression, meaning that the answer is .

2

What are the solutions to $y = x^{2} + x -6$ ?

Explanation

When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of such that the output will be zero. Thus, we first factor the equation.

$0 = x^{2} + x - 6 = (x+3)(x-2)$

Then, we are looking for the values where each of these factors are equal to zero.

implies

and implies

Thus, these are our solutions.

3

A polyomial with leading term $x^{3}$ has 6 as a triple root. What is this polynomial?

$x ^{3} - 18 x^{2}+ 108x -216$

$x ^{3} + 18 x^{2}+ 108x +216$

$x ^{3} -216$

$x ^{3} +216$

$x ^{3} + 18 x^{2}- 108x -216$

Explanation

Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is $(x-6)^{3}$ , which we can expland using the cube of a binomial pattern.

$(x-6)^{3} =x ^{3} - 3\cdot x^{2} \cdot 6 + 3\cdot x\cdot 6 ^{2} -6^{3}$

$x ^{3} - 18 x^{2}+ 108x -216$

4

A polyomial with leading term $x^ {3}$ has 5 and 7 as roots; 7 is a double root. What is this polynomial?

$x^{3} - 19x^{2} + 119x -245$

$x^{3} -12x^{2} + 35x$

$x^{3}+ 19x^{2} +119x +245$

$x^{3}+ 17x^{2} +95x +175$

$x^{3}- 17x^{2} +95x -175$

Explanation

Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is $(x-5)(x-7)^{2}$ . To put this in expanded form:

$(x-7)^{2} = x^{2} - 2 \cdotx\cdot 7 + 7^{2} = x^{2} - 14x + 49$

$(x-5)(x-7)^{2} =(x-5) \left ( x^{2} - 14x + 49 \right )$

$=x \left ( x^{2} - 14x + 49 \right ) -5\left( x^{2} - 14x + 4 9 \right )$

$= x^{3} - 14x^{2} + 49x - \left( 5x^{2} - 70x + 245 \right )$

$= x^{3} - 14x^{2} + 49x - 5x^{2} + 70x -245$

$= x^{3} - 19x^{2} + 119x -245$

Return to subject