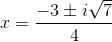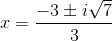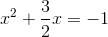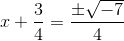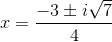Quadratic Equations and Inequalities

Help Questions

Math › Quadratic Equations and Inequalities

Questions 1 - 10

1

Solve:

$(-\infty, -4)$

$(8, \infty)$

$(10, \infty)$

Explanation

Start by setting the inequality to zero and by solving for .

Now, plot these two points on to a number line.

Notice that these two numbers effectively divide up the number line into three regions:

$(-\infty, -4)$ , , and $(8, \infty)$

Now, choose a number in each of these regions and put it back in the factored inequality to see which cases are true.

For $(-\infty, -4)$ , let

Since this is not less than , the solution to this inequality cannot lie in this region.

For , let .

Since this will make the inequality true, the solution can lie in this region.

Finally, for $(8, \infty)$ , let

Since this number is not less than zero, the solution cannot lie in this region.

Thus, the solution to this inequality is

2

Josephine wanted to solve the quadratic equation below by completing the square. Her first two steps are shown below:

Equation:

Step 1:

Step 2:

Which of the following equations would best represent the next step in solving the equation?

Explanation

To solve an equation by completing the square, you must factor the perfect square. The factored form of is . Once the left side of the equation is factored, you may take the square root of both sides.

3

Solve the expression:

Explanation

Use the FOIL method to simplify this expression.

Multiply each term of the first binomial with the terms of the second binomial.

Simplify the expression.

Combine like terms.

The answer is:

4

Evaluate the roots for:

$\frac{1}{2}\pm\frac{i\sqrt3}{2}$

$\frac{1}{4}\pm\frac{i\sqrt3}{4}$

$\frac{1}{4}\pm\frac{i\sqrt6}{4}$

$\frac{1}{3}\pm\frac{i\sqrt6}{3}$

$\frac{1}{4}\pm\frac{3i\sqrt3}{2}$

Explanation

Write the quadratic formula.

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

The coefficients of the variables can be determined by the given equation in standard form: .

Substitute the terms into the equation.

$x=\frac{-(-2)\pm\sqrt{(-2)^2-4(2)(2)}}{2(2)} = \frac{2\pm\sqrt{4-16}}{4}$

Simplify the terms.

$\frac{2\pm\sqrt{4-16}}{4} = \frac{2\pm\sqrt{-12}}{4} = \frac{2\pm 2i\sqrt{3}}{4}$

The answer is: $\frac{1}{2}\pm\frac{i\sqrt3}{2}$

5

Solve for the roots:

$\frac{1\pm\sqrt{5}}{4}$

$\frac{-1\pm\sqrt{5}}{4}$

$\frac{-1\pm i\sqrt{5}}{4}$

$\frac{-1\pm\sqrt{5}}{2}$

$\frac{1\pm\sqrt{5}}{16}$

Explanation

Write the quadratic formula.

$x= \frac{-b\pm\sqrt{b^2-4ac}}{2a}$

The given equation is in standard form of:

The coefficients correspond to the values that go inside the quadratic equation.

Substitute the values into the equation.

$x= \frac{-(-4)\pm\sqrt{(-4)^2-4(8)(-2)}}{2(8)}$

Simplify this equation.

$x= \frac{4\pm\sqrt{16+64}}{16} = \frac{4\pm\sqrt{80}}{16}$

The radical can be rewritten as:

$\sqrt{80} = \sqrt{16}\cdot \sqrt 5 = 4\sqrt5$

Substitute and simplify the fraction.

$x=\frac{4\pm4\sqrt{5}}{16}=\frac{1\pm\sqrt{5}}{4}$

The answer is: $\frac{1\pm\sqrt{5}}{4}$

6

Use the quadratic formula to determine a root:

$\frac{1-i\sqrt{35}}{6}$

$\frac{1-i\sqrt{35}}{2}$

$\frac{1-i\sqrt{37}}{6}$

$\frac{1-i\sqrt{37}}{2}$

$\frac{1-i\sqrt{37}}{3}$

Explanation

Write the quadratic formula for polynomials in the form of

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

Substitute the known values.

$x=\frac{-(-1)\pm\sqrt{(-1)^2-4(3)(3)}}{2(3)}$

Simplify the equation.

$x=\frac{1\pm\sqrt{1-36}}{6} = \frac{1\pm\sqrt{-35}}{6}= \frac{1\pm i\sqrt{35}}{6}$

The roots to this parabola is: $x= \frac{1\pm i\sqrt{35}}{6}$

The answer is $\frac{1-i\sqrt{35}}{6}$ .

7

Complete the square:

$x=\frac{-3 \pm i\sqrt{7}}{4}$

$x=\frac{-2 \pm i\sqrt{7}}{4}$

$x=\frac{-1 \pm i\sqrt{7}}{4}$

$x=\frac{-3 \pm i\sqrt{7}}{3}$

$x=\frac{-2 \pm i\sqrt{7}}{3}$

Explanation

Begin by dividing the equation by and subtracting from each side:

$x^2+\frac{3}{2}x = -1$

Square the value in front of the and add to each side:

$x^2+\frac{3}{2}x +\frac{9}{16} = -1+\frac{9}{16}$

Factor the left side of the equation:

$(x+\frac{3}{4})^2 = \frac{-7}{16}$

Take the square root of both sides and simplify:

$x+\frac{3}{4} = \frac{\pm \sqrt{-7}}{4}$

$x = \frac{-3 \pm i\sqrt{7}}{4}$

8

Find the zeros of ?

$x=-1, -\frac{1}{2}$

$x=1, -\frac{1}{2}$

$x=1, -\frac{3}{4}$

$x=-1, -\frac{3}{4}$

$x=1, \frac{3}{4}$

Explanation

This specific function cannot be factored, so use the quadratic equation:

$\frac{-b\pm \sqrt{b^2 -4ac}}{2a}$

Our function is in the form where,

Therefore the quadratic equation becomes,

$\frac{-3\pm \sqrt{3^2 -4(2)(1)}}{2(2)}$

$\frac{-3\pm \sqrt{9 -8}}{4}$

$\frac{-3\pm \sqrt{1}}{4}$

$\frac{-3+1}{4}$ OR $\frac{-3-1}{4}$

$\frac{-2}{4}$ OR $\frac{-4}{4}$

$x=-\frac{1}{2}$ OR

9

Find the zeros of ?

$x=-1, -\frac{1}{2}$

$x=1, -\frac{1}{2}$

$x=1, -\frac{3}{4}$

$x=-1, -\frac{3}{4}$

$x=1, \frac{3}{4}$

Explanation

This specific function cannot be factored, so use the quadratic equation:

$\frac{-b\pm \sqrt{b^2 -4ac}}{2a}$

Our function is in the form where,

Therefore the quadratic equation becomes,

$\frac{-3\pm \sqrt{3^2 -4(2)(1)}}{2(2)}$

$\frac{-3\pm \sqrt{9 -8}}{4}$

$\frac{-3\pm \sqrt{1}}{4}$

$\frac{-3+1}{4}$ OR $\frac{-3-1}{4}$

$\frac{-2}{4}$ OR $\frac{-4}{4}$

$x=-\frac{1}{2}$ OR

10

Expand:

$3x^{2}-25x-18$

$3x^{2}-29x-18$

$3x^{2}-18x-29$

$3x^{2}-18x-25$

None of the other answers

Explanation

To multiple these binomials, you can use the FOIL method to multiply each of the expressions individually.This will give you

or $3x^{2}-25x-18$ .

Page 1 of 100

Return to subject

AI TutorYour personal study buddy

Questions of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Practice TestsTest your skills with exam questions

QuizzesTest your knowledge with a quiz

GamesLearn through free games