Pre-Calculus
Help Questions
Math › Pre-Calculus
What is the domain of the function below:
**
Explanation
The domain is defined as the set of possible values for the x variable. In order to find the impossible values of x, we should:
a) Set the equation under the radical equal to zero and look for probable x values that make the expression inside the radical negative:
There is no real value for x that will fit this equation, because any real value square is a positive number i.e. cannot be a negative number.
b) Set the denominator of the fractional function equal to zero and look for probable x values:
Now we can solve the equation for x:
There is no real value for x that will fit this equation.
The radical is always positive and denominator is never equal to zero, so the f(x) is defined for all real values of x. That means the set of all real numbers is the domain of the f(x) and the correct answer is 
Alternative solution for the second part of the solution:
After figuring out that the expression under the radical is always positive (part a), we can solve the radical and therefore denominator for the least possible value (minimum value). Setting the x value equal to zero will give the minimum possible value for the denominator.
That means the denominator will always be a positive value greater than 1/2; thus it cannot be equal to zero by setting any real value for x. Therefore the set of all real numbers is the domain of the f(x).
Simplify the following polynomial function:
Explanation
First, multiply the outside term with each term within the parentheses:
Rearranging the polynomial into fractional form, we get:
What are the solutions to 
Explanation
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of 
Then, we are looking for the values where each of these factors are equal to zero.

and 
Thus, these are our solutions.
Factor the polynomial if the expression is equal to zero when 
Explanation
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression 
Now we need to check the answer.
We are able to get back to the original expression, meaning that the answer is 
What is the center and radius of the circle indicated by the equation?
Explanation
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 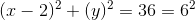


What is the domain of the function below?
Explanation
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:
The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:
Therefore, the domain is 
Calculate 
The limit does not exist.
Explanation
This can be rewritten as follows:
We can substitute 



Explanation
Solve 
Explanation
First we start by subtracting 
Next, we rewrite the equation in exponent form:
Finally, we divide by 
What is the domain of the function below?
Explanation
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:
The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:
Therefore, the domain is 
![f(x)=\frac{1}{\sqrt[4]{x^{2}+1}-\frac{1}{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138723/gif.latex)




![\sqrt[4]{x^2+1}-\frac{1}{2}=0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93233/gif.latex)


![\sqrt[4]{x^2+1}-\frac{1}{2}=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93235/gif.latex)
![\sqrt[4]{0+1}-\frac{1}{2}=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138727/gif.latex)


























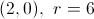

















![= \lim_{x\rightarrow \infty }\left [\left ( x^{2}-1 \right ) \cdot \sin \frac{1}{ x^{2}-1} \right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99922/gif.latex)
















