$\bigtriangleup ABC$ is an equilateral triangle; $\bigtriangleup DEF$ is an equiangular triangle.

True or false: From the given information, it follows that $\bigtriangleup ABC \sim \bigtriangleup DEF$ .

True

False

Explanation

As we are establishing whether or not $\bigtriangleup ABC \sim \bigtriangleup DEF$ , then , , and correspond respectively to , , and .

A triangle is equilateral (having three sides of the same length) if and only if it is also equiangular (having three angles of the same measure, each of which is $60^{\circ }$ ). It follows that all angles of both triangles measure $60^{\circ }$ .

Specifically, $\angle A \cong \angle D$ and $\angle B \cong \angle E$ , making two pairs of corresponding angles congruent. By the Angle-Angle Similarity Postulate, it follows that $\bigtriangleup ABC \sim \bigtriangleup DEF$ , making the correct answer "true".

2

Rhombus_1

The above figure shows a rhombus . Give its area.

$40 \sqrt{11}$

$40\sqrt{61}$

Explanation

Construct the other diagonal of the rhombus, which, along with the first one, form a pair of mutual perpendicular bisectors.

Rhombus_1

By the Pythagorean Theorem,

$n = \sqrt{12^{2}- 10^{2}} =\sqrt{144- 100} = \sqrt{44}= \sqrt{4}\cdot \sqrt{11} = 2 \sqrt{11}$

The rhombus can be seen as the composite of four congruent right triangles, each with legs 10 and $2 \sqrt{11}$ , so the area of the rhombus is

$A = 4 \cdot \frac{1}{2}\cdot 10 \cdot 2\sqrt{11} =40 \sqrt{11}$ .

3

A square with a side length of 4 inches is inscribed in a circle, as shown below. What is the area of the unshaded region inside of the circle, in square inches?

Act_math_01

8π - 16

4π-4

8π-4

2π-4

8π-8

Explanation

Using the Pythagorean Theorem, the diameter of the circle (also the diagonal of the square) can be found to be 4√2. Thus, the radius of the circle is half of the diameter, or 2√2. The area of the circle is then π(2√2)2, which equals 8π. Next, the area of the square must be subtracted from the entire circle, yielding an area of 8π-16 square inches.

4

Each side of this pentagon has a length of .

Solve for the area of the pentagon.

Varsity record

Explanation

The formula for area of a pentagon is $A=5\cdot(\frac{1}{2}\cdot s\cdot h)$ , with representing the length of one side and representing the apothem.

To find the apothem, we can convert our one pentagon into five triangles and solve for the height of the triangle:

Varsity record

Each of these triangles have angle measures of $72$^{\circ}$; 54$^{\circ}$;54$^{\circ}$$ , with $72$^{\circ}$$ being the angle oriented around the vertex. This is because the polygon has been divided into five triangles and $\frac{360}{5}= 72$ .

Varsity pentagon

To solve for the apothem, we can use basic trigonometric ratios:

$tan(54$^{\circ}$)= 1.3764$

$\1.3764=\frac{x}{2.5;cm}\x=3.44;cm$

Now that we know the apothem length, we can plug in all our values to solve for area:

$Area=5\cdot\frac{1}{2}\cdot 5;cm \cdot3.44;cm=43;cm$

5

Find the perimeter.

Explanation

How do you find the perimeter of a right triangle?

There are three primary methods used to find the perimeter of a right triangle.

When side lengths are given, add them together.
Solve for a missing side using the Pythagorean theorem.
If we know side-angle-side information, solve for the missing side using the Law of Cosines.

Method 1:

This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

Screen shot 2016 07 07 at 11.31.44 am

If we know the lengths of sides , , and , then we can simply add them together to find the perimeter of the triangle. It is important to note several things. First, we need to make sure that all the units given match one another. Second, when all the side lengths are known, then the perimeter formula may be used on all types of triangles (e.g. right, acute, obtuse, equilateral, isosceles, and scalene). The perimeter formula is written formally in the following format:

$\textup{Perimeter}=a+b+c$

Method 2:

In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one $90^{\circ}$ angle. It is a special triangle and needs to be labeled accordingly. The legs of the triangle form the $90^{\circ}$ angle and they are labeled and . The side of the triangle that is opposite of the $90^{\circ}$ angle and connects the two legs is known as the hypotenuse. The hypotenuse is the longest side of the triangle and is labeled as .

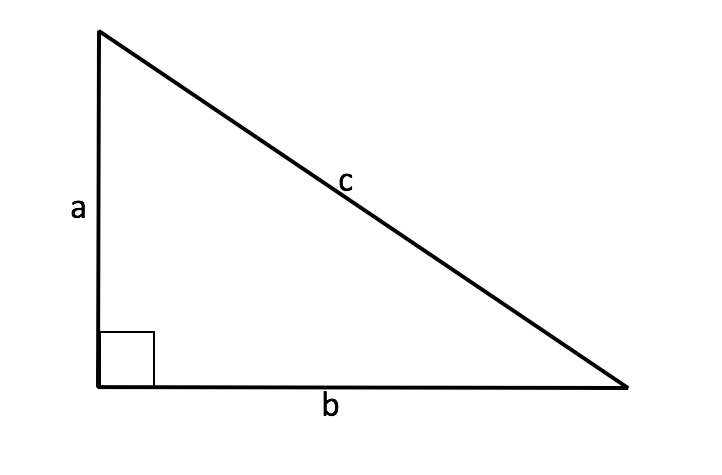
Screen shot 2016 07 07 at 10.13.54 am

If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:

We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, .

Rearrange and take the square root of both sides.

$\sqrt{c^2}=\sqrt{a^2+b^2}$

Simplify.

$c=\sqrt{a^2+b^2}$

Now, let's use the Pythagorean theorem to solve for one of the legs, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{a^2}=\sqrt{c^2-b^2}$

Simplify.

$a=\sqrt{c^2-b^2}$

Last, let's use the Pythagorean theorem to solve for the adjacent leg, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{b^2}=\sqrt{c^2-a^2}$

Simplify.

$b=\sqrt{c^2-a^2}$

It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:

$c=\sqrt{a^2+b^2}$

$a=\sqrt{c^2-b^2}$

$b=\sqrt{c^2-a^2}$

After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.

Method 3:

This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

Screen shot 2016 07 07 at 12.58.14 pm

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:

$a^2=b^2+c^2-2bc\cdot \cos A$

$b^2=a^2+c^2-2ac\cdot \cos B$

$c^2=a^2+b^2-2ab\cdot \cos C$

After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.

Solution:

Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.

In order to find the perimeter, we must first find the length of the hypotenuse of the right triangle.

Use Pythagorean's theorem to find the length of the hypotenuse:

$c=\sqrt{a^2+b^2}$

Plug in the values of the lengths of the legs of the given triangle.

$c=\sqrt{6^2+17^2}=\sqrt{325}=5\sqrt{13}$

Now, recall how to find the perimeter of a triangle:

$\text{Perimeter}=a+b+c$

Plug in all the values of the sides of the triangle to find the perimeter.

$\text{Perimeter}=6+17+5\sqrt{13}=41.03$

Make sure to round to places after the decimal.

6

Find the perimeter.

Explanation

How do you find the perimeter of a right triangle?

There are three primary methods used to find the perimeter of a right triangle.

When side lengths are given, add them together.
Solve for a missing side using the Pythagorean theorem.
If we know side-angle-side information, solve for the missing side using the Law of Cosines.

Method 1:

This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

Screen shot 2016 07 07 at 11.31.44 am

If we know the lengths of sides , , and , then we can simply add them together to find the perimeter of the triangle. It is important to note several things. First, we need to make sure that all the units given match one another. Second, when all the side lengths are known, then the perimeter formula may be used on all types of triangles (e.g. right, acute, obtuse, equilateral, isosceles, and scalene). The perimeter formula is written formally in the following format:

$\textup{Perimeter}=a+b+c$

Method 2:

In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one $90^{\circ}$ angle. It is a special triangle and needs to be labeled accordingly. The legs of the triangle form the $90^{\circ}$ angle and they are labeled and . The side of the triangle that is opposite of the $90^{\circ}$ angle and connects the two legs is known as the hypotenuse. The hypotenuse is the longest side of the triangle and is labeled as .

Screen shot 2016 07 07 at 10.13.54 am

If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:

We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, .

Rearrange and take the square root of both sides.

$\sqrt{c^2}=\sqrt{a^2+b^2}$

Simplify.

$c=\sqrt{a^2+b^2}$

Now, let's use the Pythagorean theorem to solve for one of the legs, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{a^2}=\sqrt{c^2-b^2}$

Simplify.

$a=\sqrt{c^2-b^2}$

Last, let's use the Pythagorean theorem to solve for the adjacent leg, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{b^2}=\sqrt{c^2-a^2}$

Simplify.

$b=\sqrt{c^2-a^2}$

It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:

$c=\sqrt{a^2+b^2}$

$a=\sqrt{c^2-b^2}$

$b=\sqrt{c^2-a^2}$

After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.

Method 3:

This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

Screen shot 2016 07 07 at 12.58.14 pm

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:

$a^2=b^2+c^2-2bc\cdot \cos A$

$b^2=a^2+c^2-2ac\cdot \cos B$

$c^2=a^2+b^2-2ab\cdot \cos C$

After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.

Solution:

Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.

Recall how to find the perimeter of a triangle:

$\text{Perimeter}=a+b+c$

The given triangle has of the three sides needed. Use the Pythagorean theorem to find the length of the third side.

Recall the Pythagorean theorem:

Since we are finding the length of the hypotenuse, , rewrite the equation.

$c=\sqrt{a^2+b^2}$

Plug in the values of and .

$c=\sqrt{3^2+9^2}=\sqrt{90}$

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to decimal places.

$\text{Perimeter}=3+9+\sqrt{90}=21.49$

7

Find the perimeter.

Explanation

How do you find the perimeter of a right triangle?

There are three primary methods used to find the perimeter of a right triangle.

When side lengths are given, add them together.
Solve for a missing side using the Pythagorean theorem.
If we know side-angle-side information, solve for the missing side using the Law of Cosines.

Method 1:

This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

Screen shot 2016 07 07 at 11.31.44 am

If we know the lengths of sides , , and , then we can simply add them together to find the perimeter of the triangle. It is important to note several things. First, we need to make sure that all the units given match one another. Second, when all the side lengths are known, then the perimeter formula may be used on all types of triangles (e.g. right, acute, obtuse, equilateral, isosceles, and scalene). The perimeter formula is written formally in the following format:

$\textup{Perimeter}=a+b+c$

Method 2:

In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one $90^{\circ}$ angle. It is a special triangle and needs to be labeled accordingly. The legs of the triangle form the $90^{\circ}$ angle and they are labeled and . The side of the triangle that is opposite of the $90^{\circ}$ angle and connects the two legs is known as the hypotenuse. The hypotenuse is the longest side of the triangle and is labeled as .

Screen shot 2016 07 07 at 10.13.54 am

If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:

We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, .

Rearrange and take the square root of both sides.

$\sqrt{c^2}=\sqrt{a^2+b^2}$

Simplify.

$c=\sqrt{a^2+b^2}$

Now, let's use the Pythagorean theorem to solve for one of the legs, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{a^2}=\sqrt{c^2-b^2}$

Simplify.

$a=\sqrt{c^2-b^2}$

Last, let's use the Pythagorean theorem to solve for the adjacent leg, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{b^2}=\sqrt{c^2-a^2}$

Simplify.

$b=\sqrt{c^2-a^2}$

It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:

$c=\sqrt{a^2+b^2}$

$a=\sqrt{c^2-b^2}$

$b=\sqrt{c^2-a^2}$

After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.

Method 3:

This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

Screen shot 2016 07 07 at 12.58.14 pm

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:

$a^2=b^2+c^2-2bc\cdot \cos A$

$b^2=a^2+c^2-2ac\cdot \cos B$

$c^2=a^2+b^2-2ab\cdot \cos C$

After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.

Solution:

Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.

Recall how to find the perimeter of a triangle:

$\text{Perimeter}=a+b+c$

The given triangle has of the three sides needed. Use the Pythagorean theorem to find the length of the third side.

Recall the Pythagorean theorem:

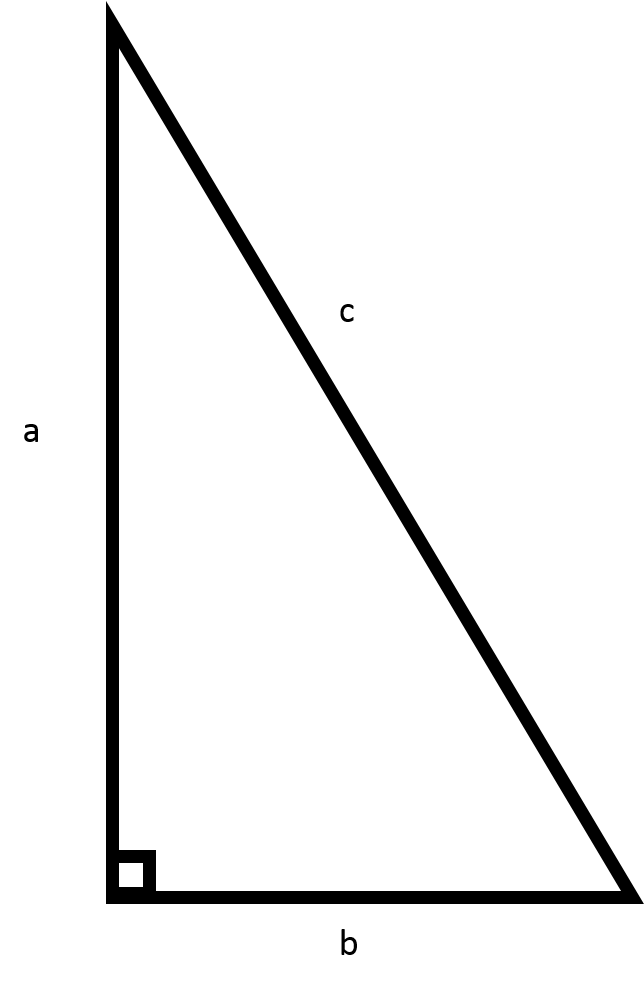
Since we are finding the length of side , rewrite the equation.

$b=\sqrt{c^2-a^2}$

Plug in the values of and .

$b=\sqrt{12^2-9^2}=\sqrt{63}$

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to decimal places.

$\text{Perimeter}=12+9+\sqrt{63}=28.94$

8

A rectangle has an area of $96 ; cm^{2}$ . The width is four less than the length. What is the perimeter?

Explanation

For a rectangle, area is and perimeter is , where is the length and is the width.

Let = length and = width.

The area equation to solve becomes , or $x^{2}-4x-96=0$ .

To factor, find two numbers the sum to -4 and multiply to -96. -12 and 8 will work:

x2 + 8x - 12x - 96 = 0

x(x + 8) - 12(x + 8) = 0

(x - 12)(x + 8) = 0

Set each factor equal to zero and solve:

or .

Therefore the length is and the width is , giving a perimeter of .

9

If the diagonal of a square is $19\sqrt2$ , what is the area of the square?

Explanation

The diagonal of a square is also the hypotenuse of a triangle whose legs are the sides of the square.

Thus, from knowing the length of the diagonal, we can use Pythagorean's Theorem to figure out the side lengths of the square.

$\text{Diagonal}^2=\text{side length}^2+\text{side length}^2$

$\text{Diagonal}^2=2(\text{side length})^2$

$(\text{side length})^2=\frac{\text{Diagonal}^2}{2}$

$\text{side length}=\frac{\text{Diagonal}}{\sqrt2}$

We can now find the side length of the square in question.

$\text{side length}=\frac{19\sqrt2}{\sqrt2}$

Simplify.

$\text{side length}=19$

Now, recall how to find the area of a square:

$\text{Area}=(\text{side length})^2$

For the square in question,

$\text{Area }=19 ^2$

Solve.

$\text{Area }=361$

10

Find the perimeter.

Explanation

How do you find the perimeter of a right triangle?

There are three primary methods used to find the perimeter of a right triangle.

When side lengths are given, add them together.
Solve for a missing side using the Pythagorean theorem.
If we know side-angle-side information, solve for the missing side using the Law of Cosines.

Method 1:

This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

Screen shot 2016 07 07 at 11.31.44 am

If we know the lengths of sides , , and , then we can simply add them together to find the perimeter of the triangle. It is important to note several things. First, we need to make sure that all the units given match one another. Second, when all the side lengths are known, then the perimeter formula may be used on all types of triangles (e.g. right, acute, obtuse, equilateral, isosceles, and scalene). The perimeter formula is written formally in the following format:

$\textup{Perimeter}=a+b+c$

Method 2:

In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one $90^{\circ}$ angle. It is a special triangle and needs to be labeled accordingly. The legs of the triangle form the $90^{\circ}$ angle and they are labeled and . The side of the triangle that is opposite of the $90^{\circ}$ angle and connects the two legs is known as the hypotenuse. The hypotenuse is the longest side of the triangle and is labeled as .

Screen shot 2016 07 07 at 10.13.54 am

If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:

We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, .

Rearrange and take the square root of both sides.

$\sqrt{c^2}=\sqrt{a^2+b^2}$

Simplify.

$c=\sqrt{a^2+b^2}$

Now, let's use the Pythagorean theorem to solve for one of the legs, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{a^2}=\sqrt{c^2-b^2}$

Simplify.

$a=\sqrt{c^2-b^2}$

Last, let's use the Pythagorean theorem to solve for the adjacent leg, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{b^2}=\sqrt{c^2-a^2}$

Simplify.

$b=\sqrt{c^2-a^2}$

It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:

$c=\sqrt{a^2+b^2}$

$a=\sqrt{c^2-b^2}$

$b=\sqrt{c^2-a^2}$

After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.

Method 3:

This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

Screen shot 2016 07 07 at 12.58.14 pm

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:

$a^2=b^2+c^2-2bc\cdot \cos A$

$b^2=a^2+c^2-2ac\cdot \cos B$

$c^2=a^2+b^2-2ab\cdot \cos C$

After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.

Solution:

Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.

In order to find the perimeter, we must first find the length of the hypotenuse of the right triangle.

Use Pythagorean's theorem to find the length of the hypotenuse:

$c=\sqrt{a^2+b^2}$

Plug in the values of the lengths of the legs of the given triangle.

$c=\sqrt{5^2+10^2}=\sqrt{125}=5\sqrt5$

Now, recall how to find the perimeter of a triangle:

$\text{Perimeter}=a+b+c$

Plug in all the values of the sides of the triangle to find the perimeter.

$\text{Perimeter}=5+10+5\sqrt5=26.18$

Make sure to round to places after the decimal.

Plane Geometry

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

How do you find the perimeter of a right triangle?

Method 1:

Method 2:

Method 3:

Solution:

Explanation

How do you find the perimeter of a right triangle?

Method 1:

Method 2:

Method 3:

Solution:

Explanation

How do you find the perimeter of a right triangle?

Method 1:

Method 2:

Method 3:

Solution:

Explanation

Explanation

Explanation

How do you find the perimeter of a right triangle?

Method 1:

Method 2:

Method 3:

Solution: