How to find an angle of a line
Help Questions
Math › How to find an angle of a line

Examine the diagram. Which of these conditions does not prove that 

Any of these statements can be used to prove that 
Explanation
If 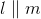
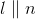

If 


If 


However, 


Lines A and B are parallel. Find the measurement of 

The measurement of 
Explanation
When parallel lines are cut by a transversal, corresponding angles are congruent. The given angle and 


AB and CD are two parrellel lines intersected by line EF. If the measure of angle 1 is 
Explanation
The angles are equal. When two parallel lines are intersected by a transversal, the corresponding angles have the same measure.
If lines A and B are parallel, what is the measurement of 

Explanation


Subtracting 78 from each side to find the measurement of angle two.
Mark is training for cross country and comes across a new hill to run on. After Mark runs 


Cannot be determined
The same as the angle of inclination
Explanation
Upon reading the question, we're left with this spatial image of Mark in our heads. After adding in the given information, the image becomes more like
The hill Mark is running on can be seen in terms of a right triangle. This problem quickly becomes one that is asking for a mystery angle given that the two legs of the triangle are given. In order to solve for the angle of depression, we have to call upon the principles of the tangent function. Tan, Sin, or Cos are normally used when there is an angle present and the goal is to calculate one of the sides of the triangle. In this case, the circumstances are reversed.
Remember back to "SOH CAH TOA." In this problem, no information is given about the hypotenuse and nor are we trying to calculate the hypotenuse. Therefore, we are left with "TOA." If we were to check, this would work out because the angle at Mark's feet has the information for the opposite side and adjacent side.
Because there's no angle given, we must use the principles behind the tan function while using a fraction composed of the given sides. This problem will be solved using arctan (sometimes denoted as 
Lines 



Explanation
When two lines are parallel, corresponding angles are congruent. Because we don't know if lines 

With the given information, we can ignore line 



If lines A and B are parallel, what is the measurement of angle 5?

Explanation

Notice that 


Now, notice that 
Thus,
If lines A and B are parallel, what is the measurement of 

Explanation

Notice that 

Now, notice that 

If 

A student creates a challenge for his friend. He first draws a square, the adds the line for each of the 2 diagonals. Finally, he asks his friend to draw the circle that has the most intersections possible.
How many intersections will this circle have?
Explanation
The answer to this problem is 12. This can be drawn as shown below (intersections marked in red).

We can also be sure that this is the maximal case because it is the largest answer selection. Were it not given as a multiple choice question, however, we could still be sure this was the largest. This is because no line can intersect a circle in more than 2 points. Keeping this in mind, we look at the construction of our initial shape. The square has 4 lines, and then each diagonal is an additional 2. We have thus drawn in 6 lines. The maximum number of intersections is therefore going to be twice this, or 12.













 and
and  are parallel lines. Solve for
are parallel lines. Solve for  .
.










































