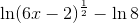First, let's begin by simplifying the left hand side.

becomes and becomes . Remember that , and the in that expression can come out to the front, as in .

Now, our expression is

From this, we can cancel out the 2's and an x from both sides.

Thus our answer becomes:

.

a)

This is exponential decay since the base, , is between and .

b)

This is exponential growth since the base, , is greater than .

Rewrite the right side as base 2.

Replace the term into the equation.

With similar bases, we can set the exponents equal.

Subtract six from both sides.

Divide by negative three on both sides.

The answer is:

You must get by itself so you must add to both side which results in

.

You must get the square root of both side to undue the exponent.

This leaves you with .

But since you square the in the equation, the original value you plug can also be its negative value since squaring it will make it positive anyway.

This means your answer can be or .

Combine the constants:

Isolate the exponential function by dividing:

Take the natural log of both sides:

Finally isolate x:

In order to condense the logarithmic expression, we use the following properties

As such

Because both sides of the equation have the same base, set the terms equal to each other.

Add 9 to both sides:

Then, subtract 2x from both sides:

Finally, divide both sides by 3:

For , our base is greater than so we have exponential growth, meaning the function is increasing. Also, when , we know that since . The only graph that fits these conditions is .

For , we have exponential growth again but when , . This is shown on graph .

For , we have exponential decay so the graph must be decreasing. Also, when , . This is shown on graph .

We expand logarithms using the same rules that we use to condense them.

Here we will use the quotient property

and the power property

.

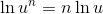
Use the quotient property:

Rewrite the radical:

Now use the power property:

The key to this is that . From here, the equation can be factored as if it were .

and

and

and

Now take the natural log (ln) of the two equations.

and

and