Functions and Graphs
Help Questions
Math › Functions and Graphs
A circle is graphed by the equation 

Explanation
First determine the center of the circle. The "x-3" portion of the circle equation tells us that the x coordinate is equal to 3. The "y-3" portion of the circle equation tells us that the y coordinate is equal to 3 as well. Therefore, the center of the circle is at (3,3).
To find the distance between (3,3) and (0,0), it is necessary to use the Pythagorean Theorem  . Where "a" and "b" are equal to 3
. Where "a" and "b" are equal to 3
(to visualize, you may draw the two points on a graph, and create a triangle. The line connecting the two points is the hypotenuse, aka "c." )
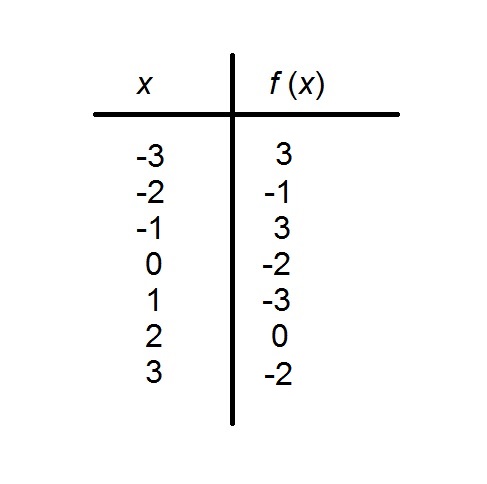
The above table shows a function with domain 
True or false: 
False
True
Explanation
A function 




If we order the rows by range value, we see this to not be the case:



What are the 
There are no 
Explanation
To find the x-intercepts of the equation, we set the numerator equal to zero.
What are the coordinates of the center of a circle with the equation 
Explanation
The equation of a circle is 
Find the slope of the following equation:
Explanation
To find the slope for a given equation, it needs to first be put into the "y=mx+b" format. Then our slope is the number in front of the x, or the "m". For this equation this looks as follows:
First subtract 2x from both sides:

That gives us the following:
Divide all three terms by three to get "y" by itself:
This means our "m" is -2/3
Which of the following is NOT a function?
Explanation
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












What is the center of the circular function 
Explanation
Remember that the "shifts" involved with circular functions are sort of like those found in parabolas. When you shift a parabola left or right, you have to think "oppositely". A right shift requires you to subtract from the x-component, and a left one requires you to add. Hence, this circle has no horizontal shift, but does shift 6 upward for the vertical component.
You can also remember the general formula for a circle with center at 

Comparing this to the given equation, we can determine the center point.
The center point is at (0,6) and the circle has a radius of 5.
Consider the following two functions:

How is the function 











Explanation
The 


Red line
Blue line
Green line
Purple line
None of them
Explanation
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to 
The blue line represents a linear function and will have a formula similar to 
The green line represents an exponential function and will have a formula similar to 
The purple line represents an absolute value function and will have a formula similar to 
Red line
Blue line
Green line
Purple line
None of them
Explanation
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to 
The blue line represents a linear function and will have a formula similar to 
The green line represents an exponential function and will have a formula similar to 
The purple line represents an absolute value function and will have a formula similar to 










































