Finding Zeros of a Polynomial
Help Questions
Math › Finding Zeros of a Polynomial
Find the roots of the function:
Explanation
Factor:
Double check by factoring:
Add together:
Therefore:
Find the zeros of the following polynomial:
Explanation
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
Solve for x.
x = 5, 2
x = –4, –3
x = –5, –2
x = 4, 3
x = 5
Explanation
- Split up the middle term so that factoring by grouping is possible.
Factors of 10 include:
1 * 10= 10 1 + 10 = 11
2 * 5 =10 2 + 5 = 7
–2 * –5 = 10 –2 + –5 = –7 Good!
- Now factor by grouping, pulling "x" out of the first pair and "-5" out of the second.
- Now pull out the common factor, the "(x-2)," from both terms.
- Set both terms equal to zero to find the possible roots and solve using inverse operations.
x – 5 = 0, x = 5
x – 2 = 0, x = 2
Find the roots of 
Explanation
If we recognize this as an expression with form 




Find the roots of the following quadratic expression:
Explanation
First, we have to know that "finding the roots" means "finding the values of x which make the expression =0." So basically we are going to set the original expression = 0 and factor.
This quadratic looks messy to factor by sight, so we'll use factoring by composition. We multiply a and c together, and look for factors that add to b.
So we can use 8 and -3. We will re-write 5x using these numbers as 8x - 3x, and then factor by grouping.
Note the extra + sign we inserted to make sure the meaning is not lost when parentheses are added. Now we identify common factors to be "pulled" out.
Now we factor out the (3x + 4).
Setting each factor = 0 we can find the solutions.
So the solutions are x = 1/2 and x = -4/3, or {-4/3, 1/2}.
Explanation
Explanation
Explanation
Consider the polynomial
Which of the following is true of the rational zeroes of 
Hint: Think "Rational Zeroes Theorem".
The only rational zeroes of 

The only rational zero of 

The only rational zero of 



Explanation
By the Rational Zeroes Theorem, any rational zeroes of a polynomial must be obtainable by dividing a factor of the constant coefficient by a factor of the leading coefficient. Since both values are equal to 1, and 1 has only 1 as a factor, this restricts the set of possible rational zeroes to the set 
Both values can be tested as follows:
1 is a zero of 


1 is indeed a zero.






















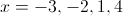
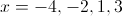
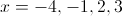

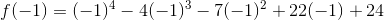





(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24))
![f(-2)=[(-2)+1][(-2)^{3}-5(-2)^{2}-2(-2)+24]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106228/gif.latex)


































































