Simplifying Trigonometric Functions - Math
Card 1 of 96
Simplify the function below:

Simplify the function below:
Tap to reveal answer
We need to use the following formulas:
a) 
and
b) 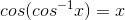
We can simplify  as follows:
as follows:

We need to use the following formulas:
a)
and
b)
We can simplify 
← Didn't Know|Knew It →
Simplify the function below:

Simplify the function below:
Tap to reveal answer
We need to use the following formulas:
a) 
and
b) 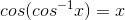
We can simplify  as follows:
as follows:

We need to use the following formulas:
a)
and
b)
We can simplify 
← Didn't Know|Knew It →
Simplify the following trionometric function:

Simplify the following trionometric function:
Tap to reveal answer
To solve the problem, you need to know the following information:



Replace the trigonometric functions with these values:





To solve the problem, you need to know the following information:
Replace the trigonometric functions with these values:
← Didn't Know|Knew It →
Change a  angle to radians.
angle to radians.
Change a 
Tap to reveal answer
In order to change an angle into radians, you must multiply the angle by  .
.
Therefore, to solve:

In order to change an angle into radians, you must multiply the angle by 
Therefore, to solve:
← Didn't Know|Knew It →
Simplify the following trigonometric function in fraction form:

Simplify the following trigonometric function in fraction form:
Tap to reveal answer
To determine the value of the expression, you must know the following trigonometric values:


Replacing these values, we get:



To determine the value of the expression, you must know the following trigonometric values:
Replacing these values, we get:
← Didn't Know|Knew It →
If  and
and  , give the value of
, give the value of  .
.
If 


Tap to reveal answer
Based on the double angle formula we have,  .
.



Based on the double angle formula we have, 
← Didn't Know|Knew It →
If  , give the value of
, give the value of  .
.
If 

Tap to reveal answer

Now we can write:




Now we can substitute the values:

Now we can write:
Now we can substitute the values:
← Didn't Know|Knew It →
If  , give the value of
, give the value of  .
.
If 

Tap to reveal answer



Now we can simplify the expression as follows:


Now we can simplify the expression as follows:
← Didn't Know|Knew It →
If  , what is the value of
, what is the value of  ?
?
If 

Tap to reveal answer
← Didn't Know|Knew It →
If  , give the value of
, give the value of  .
.
If 

Tap to reveal answer

We know that  .
.


We know that 
← Didn't Know|Knew It →
Simplify:

Simplify:
Tap to reveal answer


We know that  .
.
Then we can write:







We know that 
Then we can write:
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Simplify the following expression:

Simplify the following expression:
Tap to reveal answer
We need to use the following identities:




Use these to simplify the expression as follows:


We need to use the following identities:
Use these to simplify the expression as follows:
← Didn't Know|Knew It →
Give the value of  :
:

Give the value of 
Tap to reveal answer


Plug these values in:

Plug these values in:
← Didn't Know|Knew It →
If  , solve for
, solve for 

If 
Tap to reveal answer

Substitute  into the expression:
into the expression:



Substitute 
← Didn't Know|Knew It →
If  , give the value of
, give the value of  :
:

If 

Tap to reveal answer

Now substitute  into the expression:
into the expression:



Now substitute 
← Didn't Know|Knew It →
Simplify the following expression:

Simplify the following expression:
Tap to reveal answer
We need to use the following identitities:


Now substitute them into the expression:


We need to use the following identitities:
Now substitute them into the expression:
← Didn't Know|Knew It →
Which of the following is equal to  ?
?
Which of the following is equal to 
Tap to reveal answer
Break  apart:
apart:  .
.
This means that  or
or 
Break 

This means that 
← Didn't Know|Knew It →
Which of the following is equivalent to
 ?
?
Which of the following is equivalent to

Tap to reveal answer
In order to evaluate this expression, rewrite the trigonometric identity in terms of sines and cosines. The tangent is equal to the sine over the cosine and the cosecant is the reciprocal of the sine; thus, we can write the following:

Now, can simplify. Notice that the sine terms cancel each other out.

Remember, that the reciprocal of the cosine is the secant.

In order to evaluate this expression, rewrite the trigonometric identity in terms of sines and cosines. The tangent is equal to the sine over the cosine and the cosecant is the reciprocal of the sine; thus, we can write the following:
Now, can simplify. Notice that the sine terms cancel each other out.
Remember, that the reciprocal of the cosine is the secant.
← Didn't Know|Knew It →
Simplify: 
Simplify:
Tap to reveal answer
Rewrite  in terms of sines and cosines.
in terms of sines and cosines.

Simplify the complex fractions.


Rewrite 
Simplify the complex fractions.
← Didn't Know|Knew It →








