Whole Numbers - Math
Card 1 of 208

Simplify:
Simplify:
Tap to reveal answer
Combine like terms:  . Remember you can only combine terms that have the same variables, for example
. Remember you can only combine terms that have the same variables, for example  and
and  , but not
, but not  and
and 
Combine like terms: 



← Didn't Know|Knew It →
Simplify the expression below.

Simplify the expression below.
Tap to reveal answer
First, distribute the negative sign into the parentheses.

Next, combine like terms.

Note that all operations in this problem are addition and subtraction; there is no need to FOIL or multiply.
First, distribute the negative sign into the parentheses.
Next, combine like terms.
Note that all operations in this problem are addition and subtraction; there is no need to FOIL or multiply.
← Didn't Know|Knew It →
What is  simplified?
simplified?
What is 
Tap to reveal answer
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example,  and
and  .
.
Separate the  's to get
's to get  .
.
Then perform the necessary subtraction to get  .
.
Then separate the  's to get
's to get  .
.
Then perform the necessary subtraction to get  .
.
We then combine our answers to have the simplified version of the equation  .
.
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example, 

Separate the 

Then perform the necessary subtraction to get 
Then separate the 

Then perform the necessary subtraction to get 
We then combine our answers to have the simplified version of the equation 
← Didn't Know|Knew It →
Simplify the expression.

Simplify the expression.
Tap to reveal answer

Re-write the expression to group like terms together.

Simplify.

Re-write the expression to group like terms together.
Simplify.
← Didn't Know|Knew It →
What is  simplified?
simplified?
What is 
Tap to reveal answer
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example,  and
and 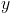 .
.
Separate the  's to get
's to get  .
.
Then perform the necessary subtraction and addition with the numbers in front of the variables to get  or
or  .
.
Then separate the 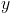 ’s to get
’s to get  .
.
Then perform the necessary subtraction to get  .
.
We then combine our answers to have the simplified version of the equation  .
.
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example, and
.
Separate the 's to get

Then perform the necessary subtraction and addition with the numbers in front of the variables to get 

Then separate the ’s to get

Then perform the necessary subtraction to get 
We then combine our answers to have the simplified version of the equation 
← Didn't Know|Knew It →
What is  simplified?
simplified?
What is 
Tap to reveal answer
To simplify a problem like the example above we must combine the like-termed variables.
Like terms are the terms that share the same variable(s) to the same power. In this example the like term is  .
.
To combine like terms the variable  stays the same and you add the numbers in front.
stays the same and you add the numbers in front.
Perform the necessary addition,  , to get
, to get  .
.
We have the simplified version of the equation,  .
.
To simplify a problem like the example above we must combine the like-termed variables.
Like terms are the terms that share the same variable(s) to the same power. In this example the like term is 
To combine like terms the variable 
Perform the necessary addition, 

We have the simplified version of the equation, 
← Didn't Know|Knew It →
Simplify the following equation into its simplest form by combining like terms:

Simplify the following equation into its simplest form by combining like terms:
Tap to reveal answer
When combining like terms, the order of operations must also be taken into account.

then combine the x squared terms to get the answer.
When combining like terms, the order of operations must also be taken into account.
then combine the x squared terms to get the answer.
← Didn't Know|Knew It →
Expand:

Expand:
Tap to reveal answer
Distribute the  by multiplying it by each term inside the parentheses.
by multiplying it by each term inside the parentheses.

and

Therefore, 5(2 + y) = 10 + 5y.
Distribute the 
and
Therefore, 5(2 + y) = 10 + 5y.
← Didn't Know|Knew It →
Which of the following is equivalent to  ?
?
Which of the following is equivalent to 
Tap to reveal answer
We need to distribute -3 by multiplying both terms inside the parentheses by -3.:
 .
.
Now we can multiply and simplify. Remember that multiplying two negative numbers results in a positive number:

We need to distribute -3 by multiplying both terms inside the parentheses by -3.:

Now we can multiply and simplify. Remember that multiplying two negative numbers results in a positive number:
← Didn't Know|Knew It →
Expand:

Expand:
Tap to reveal answer

Use the distributive property. Do not forget that the negative sign needs to be distributed as well!



Add the terms together:

Use the distributive property. Do not forget that the negative sign needs to be distributed as well!
Add the terms together:
← Didn't Know|Knew It →
Distribute:

Distribute:
Tap to reveal answer
Remember that a negative multiplied by a negative is positive, and a negative multiplied by a positive is negative.
Distribute the  through the parentheses by multiplying it by each of the two terms:
through the parentheses by multiplying it by each of the two terms:

Remember that a negative multiplied by a negative is positive, and a negative multiplied by a positive is negative.
Distribute the 
← Didn't Know|Knew It →
Simplify the expression.

Simplify the expression.
Tap to reveal answer
Multiply the mononomial by each term in the binomial, using the distributive property.




Multiply the mononomial by each term in the binomial, using the distributive property.
← Didn't Know|Knew It →
Simplify the expression.

Simplify the expression.
Tap to reveal answer

Use the distributive property to multiply each term by  .
.

Simplify.

Use the distributive property to multiply each term by 
Simplify.
← Didn't Know|Knew It →
Distribute:

Distribute:
Tap to reveal answer
When distributing with negative numbers we must remember to distribute the negative to all of the terms in the parentheses.
Remember, a negative multiplied by a negative is positive, and a negative multiplied by a positive number is negative.
Distribute the  through the parentheses:
through the parentheses:

Perform the multiplication, remembering the positive/negative rules:

When distributing with negative numbers we must remember to distribute the negative to all of the terms in the parentheses.
Remember, a negative multiplied by a negative is positive, and a negative multiplied by a positive number is negative.
Distribute the 
Perform the multiplication, remembering the positive/negative rules:
← Didn't Know|Knew It →
Find the value of  .
.
Find the value of 
Tap to reveal answer
We can seperate the problem into two steps:


We then combine the two parts:

We can seperate the problem into two steps:
We then combine the two parts:
← Didn't Know|Knew It →
Distribute  .
.
Distribute 
Tap to reveal answer
When distributing with negative numbers we must remember to distribute the negative to all of the variables in the parentheses.
Distribute the  through the parentheses by multiplying it with each object in the parentheses to get
through the parentheses by multiplying it with each object in the parentheses to get  .
.
Perform the multiplication remembering the positive/negative rules to get  , our answer.
, our answer.
When distributing with negative numbers we must remember to distribute the negative to all of the variables in the parentheses.
Distribute the 

Perform the multiplication remembering the positive/negative rules to get 
← Didn't Know|Knew It →
Simplify the expression.

Simplify the expression.
Tap to reveal answer
Use the distributive property to multiply each term of the polynomial by  . Be careful to distribute the negative as well.
. Be careful to distribute the negative as well.



Use the distributive property to multiply each term of the polynomial by 
← Didn't Know|Knew It →
Simplify the following expression:

Simplify the following expression:
Tap to reveal answer
Recall that the distributive property requires that we multiply the outside term by both terms in parentheses and add the results.

Recall that the distributive property requires that we multiply the outside term by both terms in parentheses and add the results.
← Didn't Know|Knew It →
Evaluate the following expression:

Evaluate the following expression:
Tap to reveal answer
Recall the distributive property. We need to multiply the outside factor by both terms inside and then combine.
Thus,

Recall the distributive property. We need to multiply the outside factor by both terms inside and then combine.
Thus,
← Didn't Know|Knew It →
Tap to reveal answer
Remember the order of operations: "PEMDAS” or "Please Excuse My Dear Aunt Sally" stands for "Parentheses, Exponents, Multiplication and Division, Addition and Subtraction".




Remember the order of operations: "PEMDAS” or "Please Excuse My Dear Aunt Sally" stands for "Parentheses, Exponents, Multiplication and Division, Addition and Subtraction".
← Didn't Know|Knew It →
