Other Polygons - Math
Card 1 of 92
If the area of a regular octagon is 160 and the apothem is 8, what is the side length?
If the area of a regular octagon is 160 and the apothem is 8, what is the side length?
Tap to reveal answer
To find the side length from the area of an octagon and the apothem we must use the area of a polygon which is
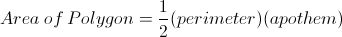
First plug in our numbers for area and the apothem to get

Then multiply to get 
Then divide both sides by 4 to get the perimeter of the figure. 
When we have the perimeter of a regular polygon, to find the side length we must divide by the number of sides of the polygon, in this case 8. 
After dividing we find the side length is 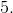
To find the side length from the area of an octagon and the apothem we must use the area of a polygon which is
First plug in our numbers for area and the apothem to get
Then multiply to get
Then divide both sides by 4 to get the perimeter of the figure.
When we have the perimeter of a regular polygon, to find the side length we must divide by the number of sides of the polygon, in this case 8.
After dividing we find the side length is
← Didn't Know|Knew It →
What is the magnitude of the interior angle of a regular nonagon?
What is the magnitude of the interior angle of a regular nonagon?
Tap to reveal answer
The equation to calculate the magnitude of an interior angle is  , where
, where  is equal to the number of sides.
is equal to the number of sides.
For our question,  .
.

The equation to calculate the magnitude of an interior angle is 

For our question, 
← Didn't Know|Knew It →
What is the interior angle measure of any regular heptagon?
What is the interior angle measure of any regular heptagon?
Tap to reveal answer
To find the angle of any regular polygon you find the number of sides,  . In this example,
. In this example,  .
.
You then subtract 2 from the number of sides yielding 5.
Take 5 and multiply it by 180 degrees to yield the total number of degrees in the regular heptagon. 
Then to find one individual angle we divide 900 by the total number of angles, 7.

The answer is  .
.
To find the angle of any regular polygon you find the number of sides, 

You then subtract 2 from the number of sides yielding 5.
Take 5 and multiply it by 180 degrees to yield the total number of degrees in the regular heptagon.
Then to find one individual angle we divide 900 by the total number of angles, 7.
The answer is 
← Didn't Know|Knew It →
A regular polygon with  sides has exterior angles that measure
sides has exterior angles that measure  each. How many sides does the polygon have?
each. How many sides does the polygon have?
A regular polygon with 

Tap to reveal answer
The sum of the exterior angles of any polygon, one per vertex, is  . As each angle measures
. As each angle measures  , just divide 360 by 1.5 to get the number of angles.
, just divide 360 by 1.5 to get the number of angles.

The sum of the exterior angles of any polygon, one per vertex, is 

← Didn't Know|Knew It →
What is the interior angle measure of any regular nonagon?
What is the interior angle measure of any regular nonagon?
Tap to reveal answer
To find the angle of any regular polygon you find the number of sides  , which in this example is
, which in this example is  .
.
You then subtract  from the number of sides yielding
from the number of sides yielding  .
.
Take  and multiply it by
and multiply it by  degrees to yield a total number of degrees in the regular nonagon.
degrees to yield a total number of degrees in the regular nonagon.

Then to find one individual angle we divide  by the total number of angles
by the total number of angles  .
.

The answer is  .
.
To find the angle of any regular polygon you find the number of sides 

You then subtract 

Take 

Then to find one individual angle we divide 

The answer is 
← Didn't Know|Knew It →
What is the measure of one exterior angle of a regular seventeen-sided polygon (nearest tenth of a degree)?
What is the measure of one exterior angle of a regular seventeen-sided polygon (nearest tenth of a degree)?
Tap to reveal answer
The sum of the measures of the exterior angles of any polygon, one per vertex, is  . In a regular polygon, all of these angles are congruent, so divide 360 by 17 to get the measure of one exterior angle:
. In a regular polygon, all of these angles are congruent, so divide 360 by 17 to get the measure of one exterior angle:

The sum of the measures of the exterior angles of any polygon, one per vertex, is 
← Didn't Know|Knew It →
What is the measure of one exterior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
What is the measure of one exterior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
Tap to reveal answer
The sum of the measures of the exterior angles of any polygon, one per vertex, is  . In a regular polygon, all of these angles are congruent, so divide 360 by 23 to get the measure of one exterior angle:
. In a regular polygon, all of these angles are congruent, so divide 360 by 23 to get the measure of one exterior angle:

The sum of the measures of the exterior angles of any polygon, one per vertex, is 
← Didn't Know|Knew It →
What is the measure of one interior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
What is the measure of one interior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
Tap to reveal answer
The measure of each interior angle of a regular polygon with  sides is
sides is  . We can substitute
. We can substitute  to obtain the angle measure:
to obtain the angle measure:

The measure of each interior angle of a regular polygon with 


← Didn't Know|Knew It →
A regular polygon has interior angles which measure  each. How many sides does the polygon have?
each. How many sides does the polygon have?
A regular polygon has interior angles which measure 
Tap to reveal answer
The easiest way to answer this is to note that, since an interior angle and an exterior angle form a linear pair - and thus, a supplementary pair - each exterior angle would have measure  . Since 360 divided by the number of sides of a regular polygon is equal to the measure of one of its exterior angles, we are seeking
. Since 360 divided by the number of sides of a regular polygon is equal to the measure of one of its exterior angles, we are seeking  such that
such that

Solve for  :
:




The polygon has 20 sides.
The easiest way to answer this is to note that, since an interior angle and an exterior angle form a linear pair - and thus, a supplementary pair - each exterior angle would have measure 

Solve for 
The polygon has 20 sides.
← Didn't Know|Knew It →
Tap to reveal answer
The perimeter of the polygon is 46. Think of this polygon as a rectangle with two of its corners "flipped" inwards. This "flipping" changes the area of the rectangle, but not its perimeter; therefore, the top and bottom sides of the original rectangle would be 12 units long (10+2=12). The left and right sides would be 11 units long (8+3=11). Adding all four sides, we find that the perimeter of the recangle (and therefore, of this polygon) is 46.
The perimeter of the polygon is 46. Think of this polygon as a rectangle with two of its corners "flipped" inwards. This "flipping" changes the area of the rectangle, but not its perimeter; therefore, the top and bottom sides of the original rectangle would be 12 units long (10+2=12). The left and right sides would be 11 units long (8+3=11). Adding all four sides, we find that the perimeter of the recangle (and therefore, of this polygon) is 46.
← Didn't Know|Knew It →
What is the perimeter of a regular nonagon with a side length of  ?
?
What is the perimeter of a regular nonagon with a side length of 
Tap to reveal answer
To find the perimeter of a regular polygon, we take the length of each side,  , and multiply it by the number of sides,
, and multiply it by the number of sides,  .
.

In a nonagon the number of sides is  , and in this example the side length is
, and in this example the side length is  .
.

The perimeter is  .
.
To find the perimeter of a regular polygon, we take the length of each side, 

In a nonagon the number of sides is 

The perimeter is 
← Didn't Know|Knew It →
What is the perimeter of a regular hendecagon with a side length of 32?
What is the perimeter of a regular hendecagon with a side length of 32?
Tap to reveal answer
To find the perimeter of a regular hendecagon you must first know the number of sides in a hendecagon is 11.
When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.
In this case it is  .
.
The answer for the perimeter is  .
.
To find the perimeter of a regular hendecagon you must first know the number of sides in a hendecagon is 11.
When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.
In this case it is 
The answer for the perimeter is 
← Didn't Know|Knew It →
Find the perimeter of the following octagon:

Find the perimeter of the following octagon:

Tap to reveal answer
The formula for the perimeter of an octagon is  .
.
Plugging in our values, we get:


The formula for the perimeter of an octagon is 
Plugging in our values, we get:
← Didn't Know|Knew It →
Tap to reveal answer
The perimeter of the polygon is 46. Think of this polygon as a rectangle with two of its corners "flipped" inwards. This "flipping" changes the area of the rectangle, but not its perimeter; therefore, the top and bottom sides of the original rectangle would be 12 units long (10+2=12). The left and right sides would be 11 units long (8+3=11). Adding all four sides, we find that the perimeter of the recangle (and therefore, of this polygon) is 46.
The perimeter of the polygon is 46. Think of this polygon as a rectangle with two of its corners "flipped" inwards. This "flipping" changes the area of the rectangle, but not its perimeter; therefore, the top and bottom sides of the original rectangle would be 12 units long (10+2=12). The left and right sides would be 11 units long (8+3=11). Adding all four sides, we find that the perimeter of the recangle (and therefore, of this polygon) is 46.
← Didn't Know|Knew It →
What is the perimeter of a regular nonagon with a side length of  ?
?
What is the perimeter of a regular nonagon with a side length of 
Tap to reveal answer
To find the perimeter of a regular polygon, we take the length of each side,  , and multiply it by the number of sides,
, and multiply it by the number of sides,  .
.

In a nonagon the number of sides is  , and in this example the side length is
, and in this example the side length is  .
.

The perimeter is  .
.
To find the perimeter of a regular polygon, we take the length of each side, 

In a nonagon the number of sides is 

The perimeter is 
← Didn't Know|Knew It →
What is the perimeter of a regular hendecagon with a side length of 32?
What is the perimeter of a regular hendecagon with a side length of 32?
Tap to reveal answer
To find the perimeter of a regular hendecagon you must first know the number of sides in a hendecagon is 11.
When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.
In this case it is  .
.
The answer for the perimeter is  .
.
To find the perimeter of a regular hendecagon you must first know the number of sides in a hendecagon is 11.
When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.
In this case it is 
The answer for the perimeter is 
← Didn't Know|Knew It →
Find the perimeter of the following octagon:

Find the perimeter of the following octagon:

Tap to reveal answer
The formula for the perimeter of an octagon is  .
.
Plugging in our values, we get:


The formula for the perimeter of an octagon is 
Plugging in our values, we get:
← Didn't Know|Knew It →
Tap to reveal answer
The perimeter of the polygon is 46. Think of this polygon as a rectangle with two of its corners "flipped" inwards. This "flipping" changes the area of the rectangle, but not its perimeter; therefore, the top and bottom sides of the original rectangle would be 12 units long (10+2=12). The left and right sides would be 11 units long (8+3=11). Adding all four sides, we find that the perimeter of the recangle (and therefore, of this polygon) is 46.
The perimeter of the polygon is 46. Think of this polygon as a rectangle with two of its corners "flipped" inwards. This "flipping" changes the area of the rectangle, but not its perimeter; therefore, the top and bottom sides of the original rectangle would be 12 units long (10+2=12). The left and right sides would be 11 units long (8+3=11). Adding all four sides, we find that the perimeter of the recangle (and therefore, of this polygon) is 46.
← Didn't Know|Knew It →
What is the perimeter of a regular nonagon with a side length of  ?
?
What is the perimeter of a regular nonagon with a side length of 
Tap to reveal answer
To find the perimeter of a regular polygon, we take the length of each side,  , and multiply it by the number of sides,
, and multiply it by the number of sides,  .
.

In a nonagon the number of sides is  , and in this example the side length is
, and in this example the side length is  .
.

The perimeter is  .
.
To find the perimeter of a regular polygon, we take the length of each side, 

In a nonagon the number of sides is 

The perimeter is 
← Didn't Know|Knew It →
What is the perimeter of a regular hendecagon with a side length of 32?
What is the perimeter of a regular hendecagon with a side length of 32?
Tap to reveal answer
To find the perimeter of a regular hendecagon you must first know the number of sides in a hendecagon is 11.
When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.
In this case it is  .
.
The answer for the perimeter is  .
.
To find the perimeter of a regular hendecagon you must first know the number of sides in a hendecagon is 11.
When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.
In this case it is 
The answer for the perimeter is 
← Didn't Know|Knew It →
