Other Polyhedrons - Math
Card 0 of 32
Find the surface area of the following half-cylinder.
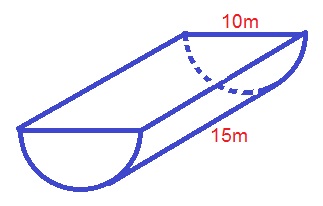
Find the surface area of the following half-cylinder.

Tap to see back →
The formula for the surface area of a half-cylinder must include one-half of the surface area of a cylinder, which would be:

We also need to add the area of the new rectangular face that is created by cutting the cylinder in half. The area of this rectangle would be:

where the length of the rectangle is the same as the height of the half-cylinder, and the width of the rectangle is the same as the diameter of the base of the half-cylinder. So we can rewrite the area of the rectangle as:

Now we can combine the two area formulas to find the total surface area of the half-cylinder:


where  is the radius of the base and
is the radius of the base and  is the length of the height, and
is the length of the height, and  is the diameter of the base.
is the diameter of the base.
Plugging in our values, we get:


The formula for the surface area of a half-cylinder must include one-half of the surface area of a cylinder, which would be:
We also need to add the area of the new rectangular face that is created by cutting the cylinder in half. The area of this rectangle would be:
where the length of the rectangle is the same as the height of the half-cylinder, and the width of the rectangle is the same as the diameter of the base of the half-cylinder. So we can rewrite the area of the rectangle as:
Now we can combine the two area formulas to find the total surface area of the half-cylinder:
where 


Plugging in our values, we get:
Find the surface area of the following polyhedron.

Find the surface area of the following polyhedron.

Tap to see back →
The formula for the surface area of the polyhedron is:



Where  is the radius of the cone,
is the radius of the cone,  is the slant height of the cone, and
is the slant height of the cone, and  is the radius of the sphere
is the radius of the sphere
Use the formula for a  triangle to find the radius and slant height:
triangle to find the radius and slant height:


Plugging in our values, we get:



The formula for the surface area of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Find the surface area of the following polyhedron.

Find the surface area of the following polyhedron.

Tap to see back →
The formula for the surface area of the polyhedron is:



where  is the radius of the cone,
is the radius of the cone,  is the slant height of the cone,
is the slant height of the cone,  is the radius of the cylinder, and
is the radius of the cylinder, and  is the height of the cylinder.
is the height of the cylinder.
Use the formula for a  triangle to find the length of the radius:
triangle to find the length of the radius:


Plugging in our values, we get:


The formula for the surface area of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Find the surface area of the following polyhedron.

Find the surface area of the following polyhedron.

Tap to see back →
The formula for the surface area of a polyhedron is:



where  is the radius of the polyhedron and
is the radius of the polyhedron and  is the slant height of the cone.
is the slant height of the cone.
Use the formula for a  triangle to find the length of the radius:
triangle to find the length of the radius:


Plugging in our values, we get:


The formula for the surface area of a polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get:
Find the volume of the following half cylinder.

Find the volume of the following half cylinder.

Tap to see back →
The formula for the volume of a half-cylinder is:

where  is the radius of the base and
is the radius of the base and  is the length of the height.
is the length of the height.
Plugging in our values, we get:


The formula for the volume of a half-cylinder is:
where 

Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:



Where  is the radius of the cone,
is the radius of the cone,  is the height of the cone, and
is the height of the cone, and  is the radius of the sphere.
is the radius of the sphere.
Use the formula for a  triangle to find the length of the radius:
triangle to find the length of the radius:


Plugging in our values, we get:



The formula for the volume of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:


where  is the radius of the cone,
is the radius of the cone,  is the height of the cone,
is the height of the cone,  is the radius of the cylinder, and
is the radius of the cylinder, and  is the height of the cylinder.
is the height of the cylinder.
Use the formula for a  triangle to find the length of the radius and height of the cone:
triangle to find the length of the radius and height of the cone:


Plugging in our values, we get:


The formula for the volume of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:


where  is the radius of the polyhedron and
is the radius of the polyhedron and  is the height of the cone.
is the height of the cone.
Use the formula for a  triangle to find the length of the radius and height:
triangle to find the length of the radius and height:


Plugging in our values, we get:


The formula for the volume of the polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get:
Find the volume of the following half cylinder.

Find the volume of the following half cylinder.

Tap to see back →
The formula for the volume of a half-cylinder is:

where  is the radius of the base and
is the radius of the base and  is the length of the height.
is the length of the height.
Plugging in our values, we get:


The formula for the volume of a half-cylinder is:
where 

Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:



Where  is the radius of the cone,
is the radius of the cone,  is the height of the cone, and
is the height of the cone, and  is the radius of the sphere.
is the radius of the sphere.
Use the formula for a  triangle to find the length of the radius:
triangle to find the length of the radius:


Plugging in our values, we get:



The formula for the volume of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:


where  is the radius of the cone,
is the radius of the cone,  is the height of the cone,
is the height of the cone,  is the radius of the cylinder, and
is the radius of the cylinder, and  is the height of the cylinder.
is the height of the cylinder.
Use the formula for a  triangle to find the length of the radius and height of the cone:
triangle to find the length of the radius and height of the cone:


Plugging in our values, we get:


The formula for the volume of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:


where  is the radius of the polyhedron and
is the radius of the polyhedron and  is the height of the cone.
is the height of the cone.
Use the formula for a  triangle to find the length of the radius and height:
triangle to find the length of the radius and height:


Plugging in our values, we get:


The formula for the volume of the polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get:
Find the volume of the following half cylinder.

Find the volume of the following half cylinder.

Tap to see back →
The formula for the volume of a half-cylinder is:

where  is the radius of the base and
is the radius of the base and  is the length of the height.
is the length of the height.
Plugging in our values, we get:


The formula for the volume of a half-cylinder is:
where 

Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:



Where  is the radius of the cone,
is the radius of the cone,  is the height of the cone, and
is the height of the cone, and  is the radius of the sphere.
is the radius of the sphere.
Use the formula for a  triangle to find the length of the radius:
triangle to find the length of the radius:


Plugging in our values, we get:



The formula for the volume of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:


where  is the radius of the cone,
is the radius of the cone,  is the height of the cone,
is the height of the cone,  is the radius of the cylinder, and
is the radius of the cylinder, and  is the height of the cylinder.
is the height of the cylinder.
Use the formula for a  triangle to find the length of the radius and height of the cone:
triangle to find the length of the radius and height of the cone:


Plugging in our values, we get:


The formula for the volume of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Find the volume of the following polyhedron.

Find the volume of the following polyhedron.

Tap to see back →
The formula for the volume of the polyhedron is:


where  is the radius of the polyhedron and
is the radius of the polyhedron and  is the height of the cone.
is the height of the cone.
Use the formula for a  triangle to find the length of the radius and height:
triangle to find the length of the radius and height:


Plugging in our values, we get:


The formula for the volume of the polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get:
Find the surface area of the following half-cylinder.

Find the surface area of the following half-cylinder.

Tap to see back →
The formula for the surface area of a half-cylinder must include one-half of the surface area of a cylinder, which would be:

We also need to add the area of the new rectangular face that is created by cutting the cylinder in half. The area of this rectangle would be:

where the length of the rectangle is the same as the height of the half-cylinder, and the width of the rectangle is the same as the diameter of the base of the half-cylinder. So we can rewrite the area of the rectangle as:

Now we can combine the two area formulas to find the total surface area of the half-cylinder:


where  is the radius of the base and
is the radius of the base and  is the length of the height, and
is the length of the height, and  is the diameter of the base.
is the diameter of the base.
Plugging in our values, we get:


The formula for the surface area of a half-cylinder must include one-half of the surface area of a cylinder, which would be:
We also need to add the area of the new rectangular face that is created by cutting the cylinder in half. The area of this rectangle would be:
where the length of the rectangle is the same as the height of the half-cylinder, and the width of the rectangle is the same as the diameter of the base of the half-cylinder. So we can rewrite the area of the rectangle as:
Now we can combine the two area formulas to find the total surface area of the half-cylinder:
where 


Plugging in our values, we get:
Find the surface area of the following polyhedron.

Find the surface area of the following polyhedron.

Tap to see back →
The formula for the surface area of the polyhedron is:



Where  is the radius of the cone,
is the radius of the cone,  is the slant height of the cone, and
is the slant height of the cone, and  is the radius of the sphere
is the radius of the sphere
Use the formula for a  triangle to find the radius and slant height:
triangle to find the radius and slant height:


Plugging in our values, we get:



The formula for the surface area of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Find the surface area of the following polyhedron.

Find the surface area of the following polyhedron.

Tap to see back →
The formula for the surface area of the polyhedron is:



where  is the radius of the cone,
is the radius of the cone,  is the slant height of the cone,
is the slant height of the cone,  is the radius of the cylinder, and
is the radius of the cylinder, and  is the height of the cylinder.
is the height of the cylinder.
Use the formula for a  triangle to find the length of the radius:
triangle to find the length of the radius:


Plugging in our values, we get:


The formula for the surface area of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Find the surface area of the following polyhedron.

Find the surface area of the following polyhedron.

Tap to see back →
The formula for the surface area of a polyhedron is:



where  is the radius of the polyhedron and
is the radius of the polyhedron and  is the slant height of the cone.
is the slant height of the cone.
Use the formula for a  triangle to find the length of the radius:
triangle to find the length of the radius:


Plugging in our values, we get:


The formula for the surface area of a polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get: