How to find the surface area of a sphere - Math
Card 1 of 144
In terms of  , give the surface area, in square inches, of a spherical water tank with a diameter of 20 feet.
, give the surface area, in square inches, of a spherical water tank with a diameter of 20 feet.
In terms of 
Tap to reveal answer
 feet =
feet =  inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set
inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set  , substitute in the surface area formula, and solve for
, substitute in the surface area formula, and solve for  :
:








← Didn't Know|Knew It →
Which is the greater quantity?
(a) The surface area of a sphere with radius 1
(b) 12
Which is the greater quantity?
(a) The surface area of a sphere with radius 1
(b) 12
Tap to reveal answer
The surface area of a sphere can be found using the formula
 .
.
The surface area of the given sphere can be found by substituting  :
:

 so
so  , or
, or 
This makes (a) greater.
The surface area of a sphere can be found using the formula

The surface area of the given sphere can be found by substituting 


This makes (a) greater.
← Didn't Know|Knew It →
Sphere A has volume  . Sphere B has surface area
. Sphere B has surface area  . Which is the greater quantity?
. Which is the greater quantity?
(a) The radius of Sphere A
(b) The radius of Sphere B
Sphere A has volume 

(a) The radius of Sphere A
(b) The radius of Sphere B
Tap to reveal answer
(a) Substitute  in the formula for the volume of a sphere:
in the formula for the volume of a sphere:





![r =\sqrt[3]{ 729} = 9](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/149269/gif.latex) inches
inches
(b) Substitute  in the formula for the surface area of a sphere:
in the formula for the surface area of a sphere:




 inches
inches
(b) is greater.
(a) Substitute 
![r =\sqrt[3]{ 729} = 9](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/149269/gif.latex)
(b) Substitute 

(b) is greater.
← Didn't Know|Knew It →
 is a positive number. Which is the greater quantity?
is a positive number. Which is the greater quantity?
(A) The surface area of a sphere with radius 
(B) The surface area of a cube with edges of length 

(A) The surface area of a sphere with radius
(B) The surface area of a cube with edges of length
Tap to reveal answer
The surface area of a sphere is  times the square of its radius, which here is
times the square of its radius, which here is  ; the surface area of the sphere in (A) is
; the surface area of the sphere in (A) is  .
.
The area of one face of a cube is the square of the length of an edge, which here is  , so the area of one face of the cube in (B) is
, so the area of one face of the cube in (B) is  . The cube has six faces so the total surface area is
. The cube has six faces so the total surface area is  .
.
 , so
, so  , giving the sphere less surface area. (B) is greater.
, giving the sphere less surface area. (B) is greater.
The surface area of a sphere is 


The area of one face of a cube is the square of the length of an edge, which here is 




← Didn't Know|Knew It →
In terms of  , give the surface area, in square inches, of a spherical water tank with a diameter of 20 feet.
, give the surface area, in square inches, of a spherical water tank with a diameter of 20 feet.
In terms of 
Tap to reveal answer
 feet =
feet =  inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set
inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set  , substitute in the surface area formula, and solve for
, substitute in the surface area formula, and solve for  :
:








← Didn't Know|Knew It →
Which is the greater quantity?
(a) The surface area of a sphere with radius 1
(b) 12
Which is the greater quantity?
(a) The surface area of a sphere with radius 1
(b) 12
Tap to reveal answer
The surface area of a sphere can be found using the formula
 .
.
The surface area of the given sphere can be found by substituting  :
:

 so
so  , or
, or 
This makes (a) greater.
The surface area of a sphere can be found using the formula

The surface area of the given sphere can be found by substituting 


This makes (a) greater.
← Didn't Know|Knew It →
Sphere A has volume  . Sphere B has surface area
. Sphere B has surface area  . Which is the greater quantity?
. Which is the greater quantity?
(a) The radius of Sphere A
(b) The radius of Sphere B
Sphere A has volume 

(a) The radius of Sphere A
(b) The radius of Sphere B
Tap to reveal answer
(a) Substitute  in the formula for the volume of a sphere:
in the formula for the volume of a sphere:





![r =\sqrt[3]{ 729} = 9](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/149269/gif.latex) inches
inches
(b) Substitute  in the formula for the surface area of a sphere:
in the formula for the surface area of a sphere:




 inches
inches
(b) is greater.
(a) Substitute 
![r =\sqrt[3]{ 729} = 9](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/149269/gif.latex)
(b) Substitute 

(b) is greater.
← Didn't Know|Knew It →
 is a positive number. Which is the greater quantity?
is a positive number. Which is the greater quantity?
(A) The surface area of a sphere with radius 
(B) The surface area of a cube with edges of length 

(A) The surface area of a sphere with radius
(B) The surface area of a cube with edges of length
Tap to reveal answer
The surface area of a sphere is  times the square of its radius, which here is
times the square of its radius, which here is  ; the surface area of the sphere in (A) is
; the surface area of the sphere in (A) is  .
.
The area of one face of a cube is the square of the length of an edge, which here is  , so the area of one face of the cube in (B) is
, so the area of one face of the cube in (B) is  . The cube has six faces so the total surface area is
. The cube has six faces so the total surface area is  .
.
 , so
, so  , giving the sphere less surface area. (B) is greater.
, giving the sphere less surface area. (B) is greater.
The surface area of a sphere is 


The area of one face of a cube is the square of the length of an edge, which here is 




← Didn't Know|Knew It →
What is the surface area of a composite figure of a cone and a sphere, both with a radius of 5 cm, if the height of the cone is 12 cm? Consider an ice cream cone as an example of the composite figure, where half of the sphere is above the edge of the cone.
What is the surface area of a composite figure of a cone and a sphere, both with a radius of 5 cm, if the height of the cone is 12 cm? Consider an ice cream cone as an example of the composite figure, where half of the sphere is above the edge of the cone.
Tap to reveal answer
Calculate the slant height height of the cone using the Pythagorean Theorem. The height will be the height of the cone, the base will be the radius, and the hypotenuse will be the slant height.



The surface area of the cone (excluding the base) is given by the formula  . Plug in our values to solve.
. Plug in our values to solve.

The surface area of a sphere is given by  but we only need half of the sphere, so the area of a hemisphere is
but we only need half of the sphere, so the area of a hemisphere is  .
.

So the total surface area of the composite figure is  .
.
Calculate the slant height height of the cone using the Pythagorean Theorem. The height will be the height of the cone, the base will be the radius, and the hypotenuse will be the slant height.
The surface area of the cone (excluding the base) is given by the formula 
The surface area of a sphere is given by 

So the total surface area of the composite figure is 
← Didn't Know|Knew It →
What is the surface area of a hemisphere with a diameter of 4 cm?
What is the surface area of a hemisphere with a diameter of 4 cm?
Tap to reveal answer
A hemisphere is half of a sphere. The surface area is broken into two parts: the spherical part and the circular base.
The surface area of a sphere is given by SA = 4pi $r^{2}$.
So the surface area of the spherical part of a hemisphere is SA = 2pi $r^{2}$.
The area of the circular base is given by A = pi $r^{2}$. The radius to use is half the diameter, or 2 cm.
A hemisphere is half of a sphere. The surface area is broken into two parts: the spherical part and the circular base.
The surface area of a sphere is given by SA = 4pi $r^{2}$.
So the surface area of the spherical part of a hemisphere is SA = 2pi $r^{2}$.
The area of the circular base is given by A = pi $r^{2}$. The radius to use is half the diameter, or 2 cm.
← Didn't Know|Knew It →
What is the surface area of a sphere with a radius of 15?
What is the surface area of a sphere with a radius of 15?
Tap to reveal answer
To solve for the surface area of a sphere you must use the equation 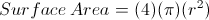
First, plug in 15 for  and square it
and square it

Multiply by 4 and  to get
to get
(%5Cpi))
The answer is  .
.
To solve for the surface area of a sphere you must use the equation
First, plug in 15 for 
Multiply by 4 and to get
The answer is 
← Didn't Know|Knew It →
What is the surface area of a sphere whise radius is  .
.
What is the surface area of a sphere whise radius is 
Tap to reveal answer
The surface area of a sphere is found by the formula  using the given radius of
using the given radius of  .
.



The surface area of a sphere is found by the formula 

← Didn't Know|Knew It →
Find the surface area of a sphere whose diameter is  .
.
Find the surface area of a sphere whose diameter is 
Tap to reveal answer
The surface area of a sphere is found by the formula  . We need to first convert the given diameter of
. We need to first convert the given diameter of  to the sphere's radius.
to the sphere's radius.



Now, we can solve for surface area.



The surface area of a sphere is found by the formula 

Now, we can solve for surface area.
← Didn't Know|Knew It →
What is the surface area of a sphere with a radius of  ?
?
What is the surface area of a sphere with a radius of 
Tap to reveal answer
To solve for the surface area of a sphere you must remember the formula: 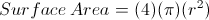
First, plug the radius into the equation for  :
:
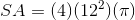
Since 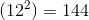 , the surface area is
, the surface area is  .
.
The answer is therefore  .
.
To solve for the surface area of a sphere you must remember the formula:
First, plug the radius into the equation for 
Since 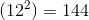

The answer is therefore 
← Didn't Know|Knew It →
To the nearest tenth of a square centimeter, give the surface area of a sphere with volume 1,000 cubic centimeters.
To the nearest tenth of a square centimeter, give the surface area of a sphere with volume 1,000 cubic centimeters.
Tap to reveal answer
The volume of a sphere in terms of its radius  is
is

Substitute  and solve for
and solve for  :
:




![r=\sqrt[3]{ $\frac{3,000}{4\pi }$} \approx 6.20 \textrm{ cm }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/100061/gif.latex)
Substitute for  in the formula for the surface area of a sphere:
in the formula for the surface area of a sphere:

The volume of a sphere in terms of its radius 
Substitute 

Substitute for 
← Didn't Know|Knew It →
Find the surface area of a sphere with a radius of  .
.
Find the surface area of a sphere with a radius of 
Tap to reveal answer
The standard equation to find the area of a sphere is  .
.
Substitute the given radius into the standard equation to get the answer:

The standard equation to find the area of a sphere is 
Substitute the given radius into the standard equation to get the answer:
← Didn't Know|Knew It →
Given that the radius of a sphere is 3, find the surface area.
Given that the radius of a sphere is 3, find the surface area.
Tap to reveal answer
The standard equation to find the area of a sphere is

where  denotes the radius. Plug in the given radius to find the surface area.
denotes the radius. Plug in the given radius to find the surface area.

The standard equation to find the area of a sphere is
where 
← Didn't Know|Knew It →
Find the surface area of the following sphere.

Find the surface area of the following sphere.

Tap to reveal answer
The formula for the surface area of a sphere is:

where  is the radius of the sphere.
is the radius of the sphere.
Plugging in our values, we get:


The formula for the surface area of a sphere is:
where 
Plugging in our values, we get:
← Didn't Know|Knew It →
Find the surface area of the following sphere.

Find the surface area of the following sphere.

Tap to reveal answer
The formula for the surface area of a sphere is:

Where  is the radius of the sphere
is the radius of the sphere
Plugging in our values, we get:


The formula for the surface area of a sphere is:
Where 
Plugging in our values, we get:
← Didn't Know|Knew It →
In terms of  , give the surface area, in square inches, of a spherical water tank with a diameter of 20 feet.
, give the surface area, in square inches, of a spherical water tank with a diameter of 20 feet.
In terms of 
Tap to reveal answer
 feet =
feet =  inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set
inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set  , substitute in the surface area formula, and solve for
, substitute in the surface area formula, and solve for  :
:








← Didn't Know|Knew It →