How to find the length of the side of a 45/45/90 right isosceles triangle - Math
Card 1 of 136
The perimeter of a 45-45-90 triangle is 100 inches. To the nearest tenth of an inch, what is the length of each leg?
The perimeter of a 45-45-90 triangle is 100 inches. To the nearest tenth of an inch, what is the length of each leg?
Tap to reveal answer
Let  be the length of a leg; then the hypotenuse is
be the length of a leg; then the hypotenuse is  , and the perimeter is
, and the perimeter is

Therefore,

Let 

Therefore,
← Didn't Know|Knew It →
Angle  in the triangle shown below is 45 degrees. Side
in the triangle shown below is 45 degrees. Side  has a length of 10. What is the length of side
has a length of 10. What is the length of side  ?
?
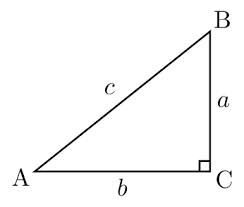
Angle 



Tap to reveal answer
Since we know two of the three angles in this triangle, we can calculate the third,  .
.

Therefore this is a 45/45/90 right triangle. Remember that 45/45/90 right triangles are have a leg:leg:hypotenuse ratio of 1:1: .
.
We know the hypotenuse,  , so we can quickly calculate the length of one of the legs,
, so we can quickly calculate the length of one of the legs,  , by dividing by
, by dividing by  :
:

To make this look like one of the answer choies, rationalize the denominator by muliplying the fraction by  :
:

Since we know two of the three angles in this triangle, we can calculate the third, 
Therefore this is a 45/45/90 right triangle. Remember that 45/45/90 right triangles are have a leg:leg:hypotenuse ratio of 1:1:
We know the hypotenuse, 


To make this look like one of the answer choies, rationalize the denominator by muliplying the fraction by 
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →
 is a
is a  triangle.
triangle.



What is the length of  ?
?



What is the length of 
Tap to reveal answer
We know that the sides of  triangles are in the ratio of
triangles are in the ratio of  , where the shorter sides lies opposite the
, where the shorter sides lies opposite the  angles, and the longer side is the hypotenuse and lies opposite the right angle. We are given that the hypotenuse is
angles, and the longer side is the hypotenuse and lies opposite the right angle. We are given that the hypotenuse is  .
.
Divide the length of the hypotenuse by  to calculate the ratio of magnification.
to calculate the ratio of magnification.

Multiply the length of the shorter sides by the ratio of magnification.

So the length of  (and
(and  ) is
) is  .
.
We know that the sides of 



Divide the length of the hypotenuse by 
Multiply the length of the shorter sides by the ratio of magnification.
So the length of 


← Didn't Know|Knew It →
The following image is not to scale.
Find the length of one of the legs of the right triangle.

The following image is not to scale.
Find the length of one of the legs of the right triangle.
Tap to reveal answer

Because of the tick marks on both legs, we can determine that this right triangle is a 45/45/90 triangle. Because the length of both legs are the same, this means that the angle opposite of each leg is also the same.
45/45/90 triangles are special, just like 30/60/90 triangles. Solving for one of the leg lengths can be determined easily through remembering the following:

Using this and the 7ft, we can solve for "s" which will provide us with the leg length.

 while this is the correct answer, the options provided are represented as simplified radicals.
while this is the correct answer, the options provided are represented as simplified radicals.

Because of the tick marks on both legs, we can determine that this right triangle is a 45/45/90 triangle. Because the length of both legs are the same, this means that the angle opposite of each leg is also the same.
45/45/90 triangles are special, just like 30/60/90 triangles. Solving for one of the leg lengths can be determined easily through remembering the following:
Using this and the 7ft, we can solve for "s" which will provide us with the leg length.

← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of the triangle?
, what is the length of a side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of this triangle?
, what is the length of a side of this triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of this triangle?
, what is the length of a side of this triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of the triangle?
, what is the length of a side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of the triangle?
, what is the length of a side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of the triangle?
, what is the length of a side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of the triangle?
, what is the length of a side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of one side of the triangle?
, what is the length of one side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of one side of the triangle?
, what is the length of one side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of one side of the triangle?
, what is the length of one side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.


Reduce.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of the triangle?
, what is the length of a side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the length of a side of the triangle?
, what is the length of a side of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
A right isosceles triangle is also a  triangle.
triangle.

To find the length of a side, we will need to use the Pythagorean Theorem:

Since this is an isosceles triangle,

The Pythagorean Theorem can then be rewritten as the following:


Since we are trying to find the length of a side of this triangle, solve for  .
.

Simplify.


Multiply the fraction by one in the form of  .
.

Solve.

Now, substitute in the length of the hypotenuse in for  to solve for the side of the triangle in the question.
to solve for the side of the triangle in the question.

Simplify.

A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
← Didn't Know|Knew It →
In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Tap to reveal answer

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.

In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.

Now, because this is a right isosceles triangle,

We can then make the following substitution:




Therefore:


Substitute in the value of the hypotenuse to find the length of the base:


Now, substitute this number in to find the area of the triangle.



Next, recall how to find the area of the rectangle:

Substitute in the given information from the question to find the area.


Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.


Solve.


In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.
In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.
Now, because this is a right isosceles triangle,
We can then make the following substitution:
Therefore:
Substitute in the value of the hypotenuse to find the length of the base:
Now, substitute this number in to find the area of the triangle.
Next, recall how to find the area of the rectangle:
Substitute in the given information from the question to find the area.
Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.
Solve.
← Didn't Know|Knew It →
In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Tap to reveal answer

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.

In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.

Now, because this is a right isosceles triangle,

We can then make the following substitution:




Therefore:


Substitute in the value of the hypotenuse to find the length of the base:


Now, substitute this number in to find the area of the triangle.



Next, recall how to find the area of the rectangle:

Substitute in the given information from the question to find the area.


Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.


Solve.


In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.
In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.
Now, because this is a right isosceles triangle,
We can then make the following substitution:
Therefore:
Substitute in the value of the hypotenuse to find the length of the base:
Now, substitute this number in to find the area of the triangle.
Next, recall how to find the area of the rectangle:
Substitute in the given information from the question to find the area.
Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.
Solve.
← Didn't Know|Knew It →




