How to find the length of the diagonal of a rectangle - Math

The diagonals of a rectangle are congruent and bisect each other. Therefore, is equidistant from all four vertices, making . The relationship between the sides is not relevant here.

Two consecutive sides of a rectangle and a diagonal form a right triangle, so the length of any diagonal can be determined using the Pythagorean Theorem, substituting :

The diagonals of a rectangle bisect each other. Therefore, the distance from a vertex to the point of intersection is half this, and .

Let and be the dimensions of the rectangle. Then

and, subsequently,

Since the product of the length and width is the area, we are looking for two numbers whose sum is 70 and whose product is 1,200; through trial and error, they are found to be 30 and 40. We can assign either to be and the other to be since the result is the same.

The length of a diagonal of the rectangle can be found by applying the Pythagorean Theorem:

A diagonal is 50 inches long; since 4 feet are equivalent to 48 inches, (A) is the greater quantity.

The length and width of the rectangle are in a ratio of 3:4, so the sides can be written as 3_x_ and 4_x_.

We also know the area, so we write an equation and solve for x:

(3_x_)(4_x_) = 12_x_2 = 108.

x2 = 9

x = 3

Now we can recalculate the length and the width:

length = 3x = 3(3) = 9 centimeters

width = 4x = 4(3) = 12 centimeters

Using the Pythagorean Theorem we can find the diagonal, c:

length2 + width2 = c2

92 + 122 = _c_2

81 + 144 = c2

225 = c2

c = 15 centimeters

The diagonal of the rectangle is equivalent to finding the length of the hypotenuse of a right triangle with sides 3 and 4. Using the Pythagorean Theorem:

$3^{2}$$+4^{2}$ = $hypotenuse^{2}$

25 = $hypotenuse^{2}$

hypotenuse = 5

Therefore the diagonal of the rectangle is 5 feet.

To find the diagonal of a rectangle we must use the side lengths to create a 90 degree triangle with side lengths of 5, 8, and a hypotenuse which is equal to the diagonal.

If we have a right angle triangle and a value for two of the three side lengths, we use the Pythagorean Theorem to solve for the length of the third side.

The two side lengths that meet to form the right angle are labeled and which are interchangeable for each side length.

The long length connecting them is labeled and is known as the hypotenuse.

The Pythagorean Theorem states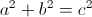

Take 5 and 8 and plug them into the equation as and to yield

First square the numbers

After squaring the numbers add them together

Once you have the sum, square root both sides

After calculating our answer for the diagonal is .

First we must find the length of the rectangle before we can solve for the diagonal. With a length shorter than twice the width, we can solve for length by drafting an algebraic equation:

Now that we know the values for length and width, we can use the Pythagorean Theorem to solve for the diagonal:

To find the diagonal of a rectangle recall that the diagonal will create a triangle where the width and length are legs of the triangle and the diagonal is the hypotenuse.

To solve, simple use the Pythagorean Theorem and solve for the hypotenuse, which will be the diagonal of the rectangle.

Thus,

To solve, simply use the Pythagorean Theorem. Thus,

To find the diagonal we use the Pythagorean Theorem:

where = hypotenuse

or

The rectangle can be cut into two equal right triangles, where the hypotenuse of both is the rectangle's diagonal.

Use the Pythagorean Theorem to find the hypotenuse:

, where a and b are the legs and c is the hypotenuse

You can find the diagonal of a rectangle if you have the width and the height. The diagonal equals the square root of the width squared plus the height squared.

1. Use Pythagorean Theorem with and .

2. Solve for , the length of the diagonal:

This rounds down to because the hundredth's place () is less than .

A diagonal of a rectangle cuts the rectangle into 2 right triangles with sides equal to the sides of the rectangle and with a hypotenuse that is the diagonal. All you need to do is use the pythagorean theorem:

where a and b are the sides of the rectangle and c is the length of the diagonal.

A picture helps greatly with this problem, so we begin with a rectangular basketball court.

We note that the distance run by Kyrie (drawn in red) is the diagonal of our rectangle, which we will call . We should also not that this diagonal divides our rectangle into two congruent right triangles. We can therefore find the length of our diagonal by focusing on one of these triangles and determining the hypotenuse. This can be done with the Pythagorean Theorem, which gives us:

Taking the square root gives us

Rounding to the nearest foot gives an answer of 98.

The diagonal of a rectangle is also the hypotenuse of a right triangle that has the length and the width of the rectangle as its legs.

We can then use the Pythgorean Theorem to find the diagonal.

For the given rectangle,

The diagonal of a rectangle is also the hypotenuse of a right triangle that has the length and the width of the rectangle as its legs.

We can then use the Pythgorean Theorem to find the diagonal.

For the given rectangle,

The diagonal of a rectangle is also the hypotenuse of a right triangle that has the length and the width of the rectangle as its legs.

We can then use the Pythgorean Theorem to find the diagonal.

For the given rectangle,

The diagonal of a rectangle is also the hypotenuse of a right triangle that has the length and the width of the rectangle as its legs.

We can then use the Pythgorean Theorem to find the diagonal.

For the given rectangle,